这一节，我们将在直角坐标系下，利用坐标变换，使二次曲线的方程在新坐标系里具有最简形式，然后在此基础上进行二次曲线的分类。

1．平面直角坐标变换

我们知道，如果平面内一点的旧坐标与新坐标分别为与，那么移轴公式为

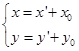                                  (5.6-1)

或

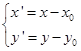                                  (5.6-1’)

式中为新坐标系原点在旧坐标系里的坐标。转轴公式为

                           (5.6-2)

或

                           (5.6-2’)

式中的为坐标轴的旋转角。

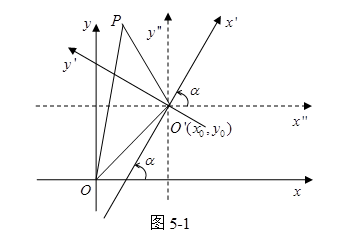
而在一般情形，由旧坐标系变成新坐标系，总可以分两步来完成，先移轴使坐标原点与新坐标系的原点重合，变成坐标系，然后由辅助坐标系再转轴而成新坐标系（图5-1）。设平面上任意点的旧坐标与新坐标分别为与，而在辅助坐标系中的坐标为，那么由（5.6-1）与（5.6-2）分别得

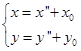
与

由上两式得一般坐标变换公式为

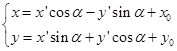                 (5.6-3)

由(5.6-3)解出便得逆变换公式

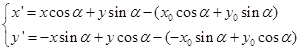        (5.6-4)

平面直角坐标变换公式(5.6-3)是由新坐标系原点的坐标与坐标轴的旋转角决定的。确定坐标变换公式，除了上面的这种情况外，还可以有其它的方法。例如给出了新坐标系的两坐标轴在旧坐标系里的方程，并规定了一个轴的正方向等。现在我们就来介绍这种情况下的坐标变换公式。

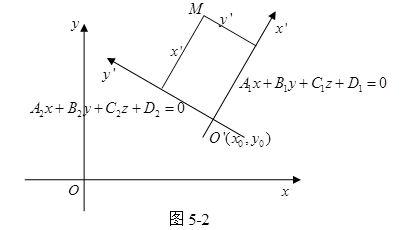
设在直角坐标系里给定了两条相互垂直的直线

其中。如果取直线为新坐标系中的横轴，而直线为纵轴，并设平面上任意点的旧坐标与新坐标分别是与。因为是点到轴的距离，也就是点到的距离（图5-2），因此我们有

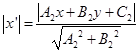
同理可得

于是在去掉绝对值符号以后，便有

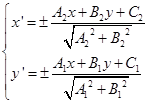                   (5.6-5)

为了使新坐标系仍然是右手坐标系，我们来决定(5.6-5)中的符号，将(5.6-5)式与公式(5.6-4)比较得

因此(5.6-5)中的第一式右端的的系数应与第二式的右端的的系数相等，所以(5.6-5)的符号选取要使得这两项的系数是同号的。

例1  已知两垂直的直线与，取为轴，为轴，求坐标变换公式。

解  设的新坐标为，那么有

根据上面的符号选取法则得变换公式为

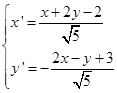  或 

前一公式由于取的，所以旋转角为小于的正角，而后一公式取的，所以旋转角为绝对值小于的负角。

2．二次曲线方程的化简与分类

设二次曲线的方程为

    （1）

现在我们要选取一个适当的坐标系，也就是要确定一个坐标变换，使得曲线（1）在新坐标系下的方程最为简单，这就是二次曲线方程的化简。为此，我们必须了解在坐标变换下二次曲线方程的系数是怎样变化的。因为一般坐标变换是由移轴与转轴组成，所以我们分别考察在移轴与转轴下，二次曲线方程（1）的系数的变换规律。

在移轴即（5.6-1）下，

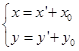
二次曲线（1）的新方程为

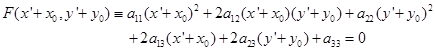
化简整理得；

这里

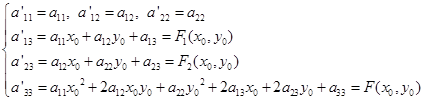   (5.6-6)

因此在移轴(5.6-1)下，二次曲线方程系数的变换规律为：

1. 二次项系数不变

2. 一次项系数变为与；

3. 常数项变为。

因为当为二次曲线（1）的中心时，有，，所以当二次曲线有中心时，作移轴，使原点与二次曲线的中心重合，那么在新坐标系下二次曲线的新方程中一次项消失。

把转轴公式(5.6-2)即

代入（1）得在转轴(5.6-2)下二次曲线（1）的新方程为

这里

进制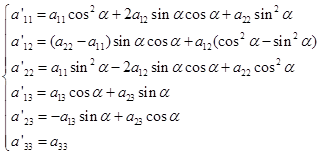      (5.6-7)

因此，在转轴下，二次曲线方程（1）的系数的变换规律为：

1) 二次项系数一般要改变。新方程的二次项系数仅与原方程的二次项系数及旋转角有关，而与一次项系数及常数项无关。

2) 一次项系数一般要改变。新方程的一次项系数仅与原方程的一次项系数及旋转角有关，与二次项系数及常数项无关，如果我们从(5.6-7)中的

解出得

那么可以进一步看到，在转轴下。，二次曲线方程（1）的一次项系数的变换规律是与点的坐标的变换规律完全一样，当原方程有一次项时，通过转轴不能完全消去一次项，当原方程无一次项时，通过转轴也不会产生一次项。

3）常数项不变。

二次曲线方程（1）里，如果，我们往往使用转轴使新方程中的。为此，我们只要取旋转角，使得

即               

所以

                       (5.6-8)

因为余切的值可以是任意的实数，所以总有满足(5.6-8)，也就是说总可以经过适当的转轴消去（1）的项。

例2  化简二次曲线方程

并画出它的图形。

解  因为二次曲线的方程含有项，因此我们总可以先通过转轴消去项。设旋转角为，那么由(5.6-8)得：

即

所以                  

从而得

取，那么，，所以得转轴公式为

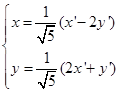
代入原方程化简整理得转轴后的新方程为

              

得用配方使上式化为

再作移轴

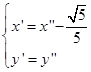
曲线方程化为最简形式。

或写成标准方程为

这是一条抛物线，它的顶点是新坐标系的原点。原方程的图形可以根据它在坐标系中的标准方程作出，它的图形如图5-3所示。

利用坐标变换化简二次曲线的方程，如果曲线有中心，那么为了计算方便，往往先移轴后转轴。

例3  化简二次曲线方程

并画出它的图形。

解  因为

，

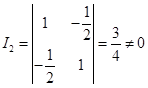所以曲线为中心二次曲线，解方程组

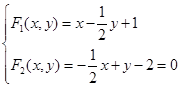
得中心的坐标为，取为新原点，作移轴

原方程变为           

再转轴消去项，由(5.6-8)得

从而可取，故转轴公式为

经转轴后曲线的方程化为最简形式

或写成标准形式

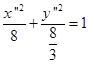
这时一个椭圆，它的图形如图5-4所示。

利用转轴来消去二次曲线方程的项，它有一个几何意义，就是把坐标轴旋转到与二次曲线的主方向平行的位置。这时因为如果二次曲线的特征根确定的主方向为，那么由(5.5-1’)立刻得：

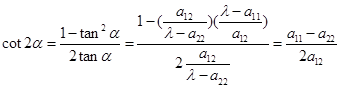
因此，上面介绍的通过转轴与称轴来化简二次曲线方程的方法，实际上是把坐标轴变换到与二次曲线的主直径（即对称轴）重合的位置。如果是中心曲线，坐标原点与曲线的中心重合；如果是无心曲线，坐标原点与曲线的顶点重合；如果是线心曲线，坐标原点可以与曲线的任何一个中心重合。因此，二次曲线方程的化简，只要先求出曲线（1）的主直径，然后以它作为新坐标轴，作坐标变换即可。

例4  化简二次曲线方程

并作出它的图形。

解  已知二次曲线的矩阵是

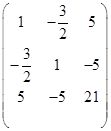
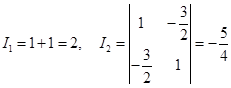
所以曲线的特征方程是

解得两特征根为

因而曲线的两个主方向为

曲线的两主直径为

与

即              与 

取这两条主直径为新坐标轴，由(5.6-5)得坐标变换公式为

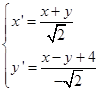
解出与

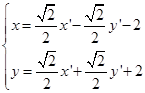
代入已知曲线方程，经过整理得曲线在新坐标系下的方程为

所以曲线的标准方程为

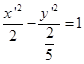
这是一条双曲线。

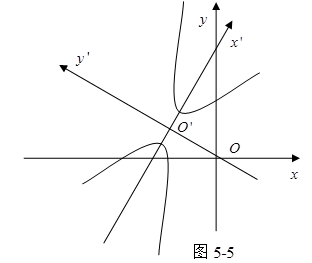
在作图时，必须首先确定轴的正向。变换公式的表达式的右端，项的系数为，项的系数为，把这些系数与公式(5.6-4)比较就知道，因此轴与轴的交角为。当新坐标系确定之后，曲线就可以在新坐标系里按标准方程作图，原方程所表示的图形如图5-5所示。

例5  化简二次曲线方程，并作出它的图形。

解  已知二次曲线的矩阵是

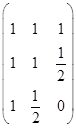
曲线为非中心曲线，它的特征方程为

特征根为              

曲线的非渐近主方向为对应于的主方向

所以曲线的主直径为

即                  

求出主直径与曲线的交点，即曲线的顶点为。所以过曲线顶点且以非渐近主方向为方向的直线为

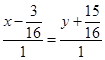  即 

这也是过顶点垂直于主直径的直线，取主直径为新坐标系的轴，而过曲线的顶点且垂直于主直径的直线为轴，作坐标变换，它的变换公式为

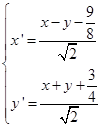
解出与

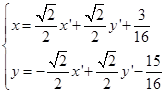
代入已知方程，经过整理得

化标准方程

这是一条抛物线。为了要画出这条抛物线，我们必须确定代表轴的直线的正向，如果轴与轴的交角为，那么根据变换公式有，因此，轴的正向就能确定了（图5-6）。

新坐标轴作出后，我们就能在新坐标系下，根据抛物线的标准方程来作出它的图形，如图5-6所示。

例6  化简。

解  已知曲线的矩阵为

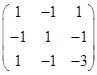
它的第一，第二两行成比例，曲线为线心曲线，它有唯一的直径即中心线，也是曲线的主直径，其方程是

取它为新坐标系的轴，再取任意垂直于这中心线的直线，比如为新坐标系的轴作坐标变换，这时的变换公式为

解出与

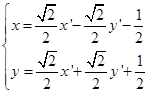
代入已知方程，经过整理得

即        或 

这是两条平行直线（图5-7）。

对于线心曲线，我们可以直接从原方程分解为两个一次因式，从而立刻可以作出它的图形。比如例5的方程可以改写为

所以                

因此原方程表示两条直线

  与 

它的图象如图5-7所示。

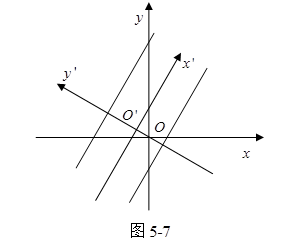
一般说来，我们有

定理1  适当选取坐标系，二次曲线的方程总可化成下列三个简化方程中的一个：

        (I) 

        (II)   

        (III) 

证  我们根据二次曲线是中心曲线、无心曲线、线心曲线三种情况来讨论。

1）当已知二次曲线为中心曲线时，我们取它的一对既共轭又互相垂直的主直径作为坐标轴建立直角坐标系。设二次曲线在这样的坐标系下的方程为

因为这时原点就是曲线的中心。所以根据定理的推论知道

其次，二次曲线的两条主直径（即坐标轴）的方向为与，它们互相共轭，因此根据(5.4-5)有

所以曲线的方程为

(I) 

又因主它是中心曲线，所以又有

2）当已知二次曲线为无心曲线时，取它的唯一直径为轴，而过顶点（即主直径与曲线的交点）且以非渐近主方向为方向的直线（即过顶点垂直于主直径的直线）为轴建立坐标系，这时的曲线方程假设为

因为这时主直径的共轭方向为，所以主直径的方程为

它就是轴，即与直线重合，所以有

又因为顶点与坐标原点重合，所以满足曲线方程，从而又有

其次，由于曲线为无心曲线，所以

而，所以有

因而曲线的方程为

(II)   

3）当已知二次曲线为线心曲线时，我们取它的中心直线（即曲线的唯一直径也是主直径）为轴，任意垂直它的直线为轴，建立坐标系。设曲线的方程为

因为线心曲线的中心直线的方程是方程

与                 

 

中的任何一个，第二个方程表示轴的条件为

而第一个方程在的条件下，不可能再表示轴，所以它必须是恒等式，因而有

所以线心曲线的方程为：

(III) 

定理证毕。

现在我们可以根据二次曲线三种简化方程系数的各种不同情况，写出二次曲线的各种标准方程，从而得出二次曲线的分类。

(I)  中心曲线

当时，那么方程可化为

其中              

如果，那么设

于是得方程

（1）  （椭圆）

如果，那么设

于是得方程

（2）（虚椭圆）

如果与异号，那么不失一般性，我们可以设，（在相反情况下，只要把两轴和对调）；设

于是得方程

（3）（双曲线）

当时，如果与同号，可以假设（在相反情况只要在方程两边同时变号），再设，于是得方程。

（4）（点或称两相交于实点的共轭虚直线）；

如果与异号，那么我们类似地有

（5）（两相交直线）

(II)  无心曲线

设，于是得方程

（6）（抛物线）。

(III)线心曲线

方程可能改写为：

当与异号，设，于得方程

（7）（两平行直线）

当与同号，设，于是得方程

（8）（两平行共轭虚直线）

当时，得方程为

（9）（两重合直线）

于是，我们得到了下面的定理。

定理2  通过适当的选取坐标系，二次曲线的方程总可以写成下面九种标准方程的一种形式：

（1）  （椭圆）

（2）（虚椭圆）

（3）（双曲线）

（4）（点或称两相交于实点的共轭虚直线）；

（5）（两相交直线）

（6）（抛物线）。

（7）（两平行直线）

（8）（两平行共轭虚直线）

（9）（两重合直线）