当前位置:课程学习>>第五章>>学习内容>>文本学习>>知识点二
知识点二:二次曲线与直线的相关位置
现在我们来讨论二次曲线
![]() (1)
(1)
与过点![]() 且具有方向
且具有方向![]() 的直线
的直线
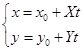 (2)
(2)
的交点。把(2)代入(1),经过整理得关于![]() 的方程
的方程
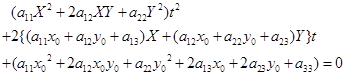 (3)
(3)
利用前面的记号,(3)可写成
![]() (4)
(4)
方程(3)或(4)可分以下几种情况来讨论。
1)![]() 。这时(4)是关于
。这时(4)是关于![]() 的二次方程,它的判别式为
的二次方程,它的判别式为
![]()
这时又可分为三种情况:
a) ![]() 。方程(4)有两个不等的实根
。方程(4)有两个不等的实根![]() 与
与![]() ,代入(2),便得直线(2)与二次曲线(1)的两相不同的实交点。
,代入(2),便得直线(2)与二次曲线(1)的两相不同的实交点。
b) ![]() 。方程(4)有两个相等的实根
。方程(4)有两个相等的实根![]() 与
与![]() ,代入(2),这时直线(2)与二次曲线(1)有两个相互重合的实交点。
,代入(2),这时直线(2)与二次曲线(1)有两个相互重合的实交点。
c) ![]() 。方程(4)有两个共轭的虚根,代入(2),这时直线(2)与二次曲线交于两个共轭的虚点。
。方程(4)有两个共轭的虚根,代入(2),这时直线(2)与二次曲线交于两个共轭的虚点。
2) ![]() ,这时又可分为三种情况:
,这时又可分为三种情况:
a) ![]() 。这时(4)是关于
。这时(4)是关于![]() 的一次方程,它有唯一的一个实根,所以直线(2)与二次曲线(1)有唯一的实交点。
的一次方程,它有唯一的一个实根,所以直线(2)与二次曲线(1)有唯一的实交点。
b) ![]() 。而
。而![]() 。这时(4)为矛盾方程,方程(4)无解,所以直线(2)与二次曲线(1)没有交点
。这时(4)为矛盾方程,方程(4)无解,所以直线(2)与二次曲线(1)没有交点
c) ![]() 。这时方程(4)成为一个恒等式,它能被任何值(实的或虚的)的
。这时方程(4)成为一个恒等式,它能被任何值(实的或虚的)的![]() 所满足,所以直线(2)上的一切点都是(1)与(2)的公共点,也就是说直线(2)全部在二次曲线上。
所满足,所以直线(2)上的一切点都是(1)与(2)的公共点,也就是说直线(2)全部在二次曲线上。
