1．二次曲线的直径

在本章第二节中我们已经讨论了直线与二次曲线相交的各种情况，当直线平行于二次曲线的某一非渐近方向时，这条直线与二次曲线总交于两点（两不同实的，两重合实的或一对共轭虚的），这两点决定了二次曲线的一条弦。现在我们来研究二次曲线上一族平行弦的中点轨迹。

定理1  二次曲线的一族平行弦的中点轨迹是一条直线.

证  设是二次曲线的一个非渐近方向，即，而是平行于方向的弦的中点，那么过的弦为

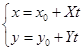
它与二次曲线的两交点（即弦的两端点）由下列二次方程

      (1)

的两根与所决定，因为弦的中点，所以有

从而有     

这就是说平行于方向的弦的中点的坐标满足方程

                      (5.4-1)

即                    (5.4-2)

或

           (5.4-3)

反过来，如果点满足方程(5.4-1)或(5.4-2)或(5.4-3)，那么方程（1）中将有绝对值等而符号相反的两个根，点就是具有方向的弦的中点，因此方程(5.4-1)或(5.4-2)或(5.4-3)为一族平行于某一非渐近方向的弦的中点轨迹方程。

方程(5.4-3)的一次项系数不能全零，这是因为当

时，将有

这与是非渐近方向的假设矛盾，所以(5.4-3)或(5.4-1)是一个二元一次方程，它是一条直线，于是定理得到了证明。

定义1  二次曲线的平行弦中点的轨迹叫做这个二次曲线的直径，它所对应的平行弦，叫做共轭于这条直径的共轭弦，而直径也叫做共轭于平行弦方向的直径。

推论  如果二次曲线的一族平行弦的斜率为，那么共轭于这族平行弦的直径方程是

                  (5.4-4)

我们从方程(5.4-1)或(5.4-4)容易看出，如果

              (2)

              (3)

表示两不同直线时，(5.4-1)或(5.4-4)将构成一直线束，当时为中心直线束，当时为平行直线束；如果（2）与（3）表示同一直线，这时，那么(5.4-1)或(5.4-4)只表示 一条直线。

如果（2）与（3）中有一为矛盾方程。比如（2）中，这时成立且(5.4-1)或(5.4-4)仍表示一平行直线束；如果（2）与（3）中有一为恒等式，比如（2）中，这时成立且(5.4-1)或(5.4-4)只表示一条直线。

因此当，即二次曲线为中心曲线时，它的全部直径属于一个中心直线束，这个直线束的中心就是二次曲线的中心；当，即二次曲线为无心曲线时，它的全部直径属于一个平行直线束，它的方向为二次曲线的渐近方向，当，即二次曲线为线心曲线时，这时二次曲线只有一条直径，它的方程是

即线心二次曲线的中心直线，因此我们有：

定理2  中心二次曲线的直径通过曲线的中心，无心二次曲线的直径平行于曲线的渐近方向，线心二次曲线的直径只有一条，就是曲线的中心直线。

例1  求椭圆或双曲线的直径。

解

根据(5.4-1)，共轭于非渐近方向的直径方程是

显然，直径通过曲线的中心。

例2  求抛物线的直径。

解             

所以共轭于非渐近方向的直径为

即                    

所以抛物线的直径平行于它的渐近方向。

例3  求二次曲线的共轭于非渐近方向的直径。

解 

直径方程为

即            

因为已知曲线的渐近方向为，所以对于非渐近方向一定有，因此曲线的共轭于非渐近方向的直径为

它只有一条直径。

2．共轭方向与共轭直径

我们把二次曲线的与非渐近方向共轭的直径方向

              (4)

叫做非渐近方向的共轭方向，所以有

共中，因此有

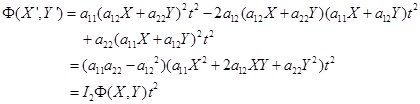
因为为非渐近方向，所以，另外又有，因此，当即二次曲线为中心曲线时，；当即二次曲线为非中心曲线时，。这就是说，中心二次曲线的非渐近方向的共轭方向仍然是非渐近方向，而在非中心二次曲线的情形是渐近方向。

由（4）得二次曲线的非渐近方向与它的共轭方向之间的关系

          (5.4-5)

从(5.4-5)式看出，两个方向与是对称的，因此对中心曲线来说，非渐近方向的共轭方向为非渐近方向，而的共轭方向就是。

定义2 中心曲线的一对具有相互共轭方向的直径叫做一对共轭直径。

设，代入(5.4-5)，得

              (5.4-6)

这就是一对共轭直径的斜率满足的关系式。

例如椭圆的一对共轭直径的斜率与有着关系

即

                       (5.4-7)

而双曲线的一对共轭直径的斜率与有着关系

                        (5.4-8)

在(5.4-5)中，如果设

那么有            

显然此时为二次曲线的渐近方向。因此如果对二次曲线的共轭方向从(5.4-5)作代数的推广，那么渐近方向可以看成与自己共轭的方向，从而渐近线也就可以看成与自己共轭的直径。