定义1  二次曲线的垂直于其共轭弦的直径叫做二次曲线的主直径，主直径的方向与垂直于主直径的方向都叫做二次曲线的主方向。

显然，主直径是二次曲线的对称轴，因此主直径也叫做二次曲线的轴，轴与曲线的交点叫做曲线的顶点。

现在我们来求二次曲线

     (1)

的主方向与主直径。

如果二次曲线（1）为中心曲线，那么与二次曲线（1）的非渐近方向共轭的直径为(5.4-1)或(5.4-3)。设直径的方向为，那么

             (2)

根据主方向的定义，成为主方向的条件是它垂直于它的共轭方向，在直角坐标系下，由(1.7-14’)得

               (3)

（3）代入（2）得

               (4)

因此成为中心二次曲线（1）的主方向的条件是

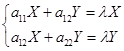                        (5.5-1)

成立，其中，或把它改写成

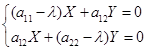                       (5.5-1’)

这时一个关于的齐次线性方程组，而不能全为零，所以

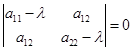                       (5.5-2)

即

                         (5.5-3)

因此对于中心二次曲线来说，只能由(5.5-3)解出，再代入(5.5-1)就能得到它的主方向。

如果二次曲线（1）为非中心二次曲线，那么它的任何直径的方向总是它的唯一的渐近方向

而垂直于它的方向显然为

所以非中心二次曲线（1）的主方向为：

渐近主方向

                   (5)

非渐近主方向

                     (6)

如果我们把(5.5-2)或(5.5-3)推广到非中心二次曲线，即式中的可取等于零，这样当时，方程(5.5-3)的两根为

把它代入(5.5-1)或(5.5-2)所得的主方向，正是非中心二次曲线的渐近主方向与非渐近主方向。

因此，一个方向成为二次曲线（1）的主方向的条件是(5.5-1)成立，这里的是方程(5.5-2)或(5.5-3)的根。

定义2  方程(5.5-2)或(5.5-3)叫做二次曲线（1）的特征方程，特征方程的根叫做二次曲线的特征根。

从二次曲线（1）的特征方程(5.5-3)求出特征根，把它代入(5.5-1)或(5.5-1’)。我们就得到相应的主方向，如果主方向为非渐近方向，那么根据(5.4-1)就能得到共轭于它的主直径。

定理1  二次曲线的特征根都是实数。

证  因为特征方程的判别式

所以二次曲线的特征根都是实数。

定理2  二次曲线的特征根不能全为零。

证  如果二次曲线的特征根全为零，那么由(5.5-3)得

即           

从而得        

这与二次曲线的定义矛盾，所以二次曲线的特征根不能全为零。

定理3  由二次曲线（1）的特征根确定的主方向，当时，为二次曲线的非渐近主方向；当时，为二次曲线的渐近主方向。

证  因为

所以由(5.5-1)得

又因为不全为零，所以当时，，为二次曲线（1）的非渐近主方向；当时，，为二次曲线（1）的渐近主方向。

定理4  中心二次曲线到少有两条主直径，非中心二次曲线只有一条主直径。

证  由二次曲线（1）的特征方程(5.5-3)解得两特征根为

1）当二次曲线（1）为中心曲线时，。如果特征方程的判别式，那么，这时的中心曲线为圆（包括点圆和虚圆），它的特征根为一对二重根。

把它代入(5.5-1)或(5.5-1’)，则得到两个恒等式，它被任何方向所满足，所以任何实方向都是圆的非渐近主方向，从而通过圆心的任何直线不仅都是直径，而且都是圆的主直径。

如果特征方程的判别式，那么特征根主两不等的非零实根，将它们分别代入

(5.5-1’)得相应的两非渐近主方向为

                    (7)

                   (8)

这两主方向相互垂直，从而它们又互相共轭，因此非圆的中心二次曲线有而且只有一对互相垂直从而又互相共轭的主直径。

2）当二次曲线（1）为非中心曲线时，，这时两特征根为

所以它只有一个非渐近的主方向，即与相应的主方向，从而非中心二次曲线只有一条主直径。

例1  求的主方向与主直径。

解  。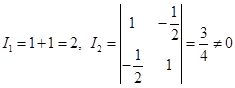

曲线为中心曲线，它的特征方程为

解这方程得两特征根为：

由特征根确定的主方向为

由特征根确定的主方向为

又因为

所以曲线的主直径为

与

即           

例2  求曲线的主方向与主直径。

解， 

曲线为非中心曲线，它的特征方程为

因此两特征根为

由这两特征根所确定的主方向为：

非渐近主方向

渐近主方向

又因为           

所以曲线的唯一主直径为

即。