学习指导

一、内容提要

1.基本概念

渐近方向、渐近线、中心、切线、直径、共轭方向、共轭弦、主方向、主直径。

2.基本结论

1）二次曲线的特征根都是实数；

2）二次曲线的特征根不能全为零；

3）由二次曲线的特征根确定的主方向，当时，为二次曲线的非渐近主方向；当时，为二次曲线的渐近主方向；

4）中心二次曲线到少有两条主直径，非中心二次曲线只有一条主直径；

5）在移轴下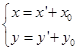

二次曲线方程系数的变换规律为：二次项系数不变；一次项系数变为与；常数项变为。

 

6）在转轴下

二次曲线方程的系数的变换规律为：

二次项系数一般要改变。新方程的二次项系数仅与原方程的二次项系数及旋转角有关，而与一次项系数及常数项无关；

   一次项系数一般要改变。新方程的一次项系数仅与原方程的一次项系数及旋转角有关，与二次项系数及常数项无关。

3.基本方法

1）坐标变换法化简二次曲线方程的方法；

2）主直径法化简二次曲线方程的方法；

3）不变量法化简二次曲线的方程的方法；

4.需要说明的问题

在解决二次曲线的化简与分类问题是，应该深刻体会坐标变换法、主直径法、不变量法研究问题的角度的异同。

二、精选例题解析

例    化简二次曲线方程：

解  因为

，

所以曲线为中心二次曲线，解方程组

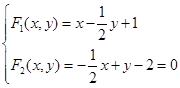
得中心的坐标为，取为新原点，作移轴

原方程变为           

再转轴消去项，由(5.6-8)得

                 

从而可取，故转轴公式为

经转轴后曲线的方程化为最简形式

或写成标准形式

。
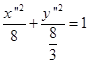