第一章  热力学第一定律

---

知识点三：准静态过程和可逆过程

一、体积功

在一定的环境压力下，当系统的体积发生变化时，系统对环境做的功（膨胀功）或环境对系统做的功（压缩功）都称为体积功。设有一汽缸的截面积为A，筒内有一无质量无磨擦力的理想活塞, 并有外力ƒe作用于活塞上，汽缸内盛有气体．若系统抵抗外力ƒe，使活塞向上移动了dl距离，则系统做的膨胀功

δW = －ƒ_e·dl(3)

因为                     ƒ_e／A = p_e 及  Adl = dV

所以                     δW = －p_edV (4)

由式(1.4)可知，外压p_e≠0及体积变化dV≠0是产生体积功的两个必要条件。若系统经过几个步骤完成整个变化，则所做的功为各步骤体积功的加和，即
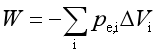                     （5）

显然，当体积变化∆V >0时，则W < 0，表示系统膨胀对环境做功；当∆V < 0时，则W > 0，表示系统体积被压缩，环境对系统做功。

在计算体积功时，不论系统压力p有多大，总是以系统对抗的外压为计算功的广义力，功等于外压p_e乘以位移。系统压力p与外压p_e的相对大小，仅用于判断系统是发生膨胀还是压缩过程。正如举重时衡量举重运动员做功的大小，总是以他能对抗外压（杠铃的重量）的大小来衡量，而不是凭他有多大“力气”；换言之，举重运动员力气的大小是要根据他能举起多重的杠铃（引起的环境变化）来判断。又如，理想气体向真空膨胀（也称自由膨胀）过程，外压p_e＝0，所以不论始态时系统的内压p有多大，功W恒为零。

二、准静态过程

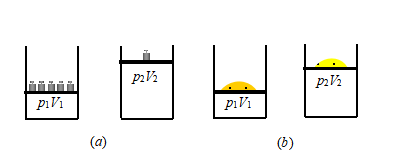
现讨论图1所示的理想气体等温膨胀过程。以带有活塞的汽缸中一定量理想气体为系统，活塞上放五个砝码，当气体的压力与重物的重量平衡时，系统处于初始平衡态，设此时气体的压力为p₁、体积为V₁，如图1(a)所示。现将砝码一次移去四个，气体的体积就会发生膨胀。开始膨胀时，靠近活塞处的压力要比其他部分气体的压力小，气体内部的压力是不均匀的，因此在膨胀过程中气体处于非平衡态，直到气体内部各处压力均为p₂的平衡态，气体的膨胀才停止。由于在膨胀过程中，系统处于非平衡状态，其状态参量没有定值，所以无法用状态参量来描述整个过程，只能描述过程的初始和终止时系统所处的平衡状态。因此在p~V图上，可分别用A点和B点来描述系统的始态和终态，见图3所示。

 

若将p₂、V₂作为始态，逆向进行上述过程，一次性加上四个砝码，使终态达到p₁、V₁的平衡态，这是一个压缩过程，同理，无法用状态参量来描述这个过程的中间状态。

设想系统从始态A经膨胀达到终态B，再经压缩回到始态A，似乎状态的变化是“可逆的”，但经过这一循环后，系统的能量又将怎样呢？膨胀时活塞与汽缸摩擦产生的热释放给了环境；在压缩时，摩擦所生的热再次释放到环境中去了, 不可能将膨胀时放到环境中的热通过压缩时的摩擦而回收，即能量没有“可逆”，最终在环境中留下了变化。

若进行分步膨胀，从图2可以看出，系统从A→B，做功W₁；再进行分步压缩，从B→A，则做功W₂；显然，︱W₂︱>︱W₁︱。说明经过一个循环后，就有︱W₂︱－︱W₁︱的能量转化为热，即环境浪费了︱W₂︱－︱W₁︱的功，才得到上述数量的热，在环境中便留下不可消除的痕迹。

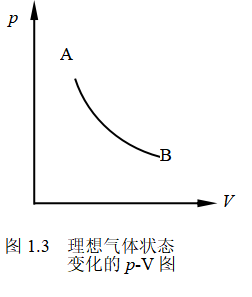
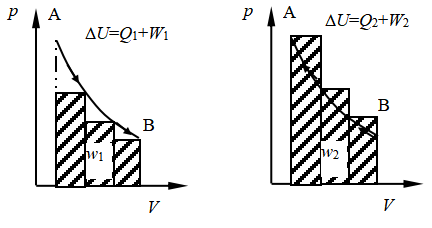
图2 膨胀（a）和压缩（b）过程的示功图

若我们设想活塞是无质量的理想活塞，而且过程进行得无限缓慢。例如，若上述膨胀过程中与始态A平衡的重物不是砝码而是无限细的砂粒，如图1(b)所示，每次膨胀时只移去一颗砂粒，使膨胀过程极其缓慢地进行，以至在过程进行的任一时刻，系统状态与平衡态的偏离总是无限小，可近似看作是平衡态。这种进行得无限缓慢，其经历的每个状态都可视为平衡态的过程，称为准静态过程。可用过程中系统状态参量的变化来描述整个准静态过程，即以一系列无限接近的描述平衡态的点来表示，实际上此过程的状态变化可用一条光滑的曲线或直线来表示，见图3所示，这样的曲线称为过程曲线。严格来说，准静态过程是一种理想过程。

三、可逆过程

无摩擦的准静态过程就是可逆过程，实际过程都是不可逆过程，两者均指的是“过程”而不是状态，它们之间的区别见表1所示。

表1 可逆过程与不可逆过程的区别

由于可逆过程的效率最高，因此可逆过程在热力学研究中有重大的理论和现实意义。实际过程通过与可逆过程的比较，可知实际过程不可逆性的程度，并能衡量提高实际过程效率的潜力。此外，一些重要的热力学函数的变化，往往需借助可逆过程才能完成具体的计算。

例2  在0℃，1mol理想气体经下列一些途径，从始态1000 kPa变化到终态100 kPa, 求各途径中气体所做的功，并在p－V图上表示出气体做功的大小。

(1)气体从始态向真空膨胀到达终态；

(2)气体从始态反抗外压100 kPa一步膨胀到达终态；

(3)气体从始态反抗外压500 kPa膨胀到达一中间态，再反抗恒外压100 kPa到达终态；

(4)气体从始态经恒温可逆膨胀到达终态。

解  按题意，过程的变化途径可如下表示：

(1)向真空膨胀，p_e = 0 ，气体不做功，即 W₁=0； 

(2)在273K时，气体反抗外压100 kPa，一步膨胀到达终态，体系所做的功为

=

=

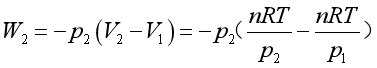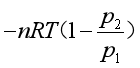
(3)气体分二步膨胀到达终态。根据式（1.5），计算过程的功为

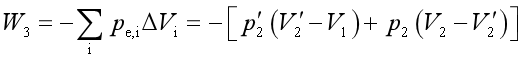
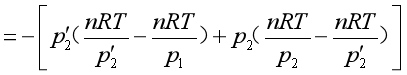
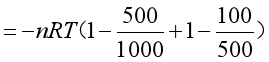
（4）恒温可逆膨胀过程。设每步膨胀都使外压p_e比系统压力p小一个无穷小量dp, 即p_e＝p－dp，系统膨胀dV，略去二级无穷小量，并代入理想气体状态方程式，则

 

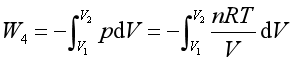
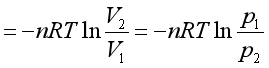
= －5226.2J

 

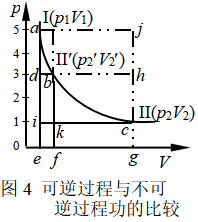
图4是以上述各过程的p－V图，从中可区分各过程所做的体积功的大小。恒温一步膨胀过程气体做的功W₂与面积S_eicg相当；等温分二步膨胀过程气体做的功W₃与面积S_efbd＋S_fgck相当；等温可逆膨胀过程气体做的功W₄与面积S_eacg相当。

上述计算结果表明，四种过程做功的大小顺序为：∣W₁∣＜∣W₂∣＜∣W₃∣＜∣W₄∣。如果将过程逆向进行，即该系统始终在外压比系统压力大dp的情况下，恒温由p₂、V₂压缩回到p₁、V₁状态，环境此时对系统做功为

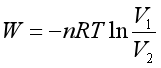
将其与W₄比较可知：系统经恒温可逆膨胀和恒温可逆压缩后，环境得的功为W₄＋W ＝0，与系统做的净功相等。系统和环境都恢复到原状态，热力学能变为△U＝0。根据热力学第一定律，则环境得热Q＝0。所以，系统经可逆变化后可恢复原状，且环境没有热和功的得失，也能恢复原状；除此以外，其它三个过程进行后，当系统恢复原状时，环境损失了功而得到了热，即在环境中留下了痕迹，所以它们均为不可逆过程。

由此可见，恒温条件下，系统对环境做的可逆膨胀功最大，环境对系统可逆压缩消耗的功最小。