第一章 热力学第一定律
知识点四： 焓和热容（热的计算）
一、等容热、等压热和焓
无论是在理论研究还是在实际化学工程中，对过程热的研究有着很重要的意义。经常遇到的是不作其他功的等容或等压条件下的热量，简称等容热QV和等压热Qp，Q的右下角注V、p分别表示等容和等压。
的等容过程，△V = 0，则W = 0，由热力学第一定律可得
△U = QV 或dU = δQV （6）
此式表明，封闭系统在不做其它功的等容过程，实验量等容热QV在量值上等于热力学能变△U。
若用右下角注1、2分别表示系统的始态和终态，在等压过程并只作体积功时，由热力学第一定律可知，等压热为
Qp= △U－W = △U＋pe△V =（U2－U1）＋pe（V2－V1）
等压过程，p1 = p2 = pe，上式可表示为:
Qp= U2－U1＋p2V2－p1V1= (U2＋p2V2)－(U1＋p1V1)
定义H = U + pV，H称为焓，则
Qp = H2 －H1 =△H ，或 δQp =dH （7）
式（7）表明，封闭系统在不做其它功的等压过程，实验量等压热Qp在量值上等于焓变△H。上述式(6)、(7)对测量和计算化学反应的焓变很有实用价值，并可使有关的数学处理简化。
由于U、p、V都是状态函数，H也一定是状态函数，在确定的始、终态间，系统的焓变△H为一定的量。焓属系统广度性质，虽具有能量单位，但其绝对量无法求得。
孤立系统的热力学能是守恒的，当系统内发生一定变化时，热力学能变△U = 0，但系统的焓变△H不一定等于零。例如，在恒容的绝热反应器中发生一个化学反应，系统不做体积功，W = 0，又因绝热，Q = 0，所以系统的热力学能变△U = 0，由于该反应器中发生了化学反应，系统的温度、压力会有变化，故系统的焓变△H≠0，显然，此时的焓变不是系统变化过程的能量变化。
二、热容
在不发生相变和化学变化的条件下，若加热一封闭系统，则系统必须吸收热。通常以测定系统温度的升高来表征其吸热的多少，显然，系统温度的升高ΔT和吸收的热Q成正比，取比例系数为
，则
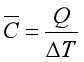
定义
为系统的平均热容，它表示在ΔT温度区间内，系统每升高单位热力学温度所需吸收的热。在不同的温度区间，系统同样升高单位热力学温度所需吸收的热不同，因此欲求在某温度时系统的热容，必须将温度区间缩至很小，即
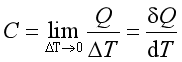（8）
热容的单位是J·K－1，它是一个广度量，与系统物质的量有关。单位质量物质的热容称为质量热容或比热，用C表示，单位为J·K－1·kg－1。单位物质的量的热容称为摩尔热容，用Cm表示，单位为J·K－1·mol－1。比热和摩尔热容均是强度量。
由于热与变化途径有关，式（1.8）中的δQ不是全微分，所以若不指定加热方式，热容是一个不确定的物理量。若在等容或等压情况下加热，它们可分别定义为等容热容CV和等压热容Cp：
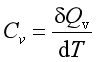和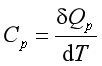
对于单位物质的量，则分别称为摩尔等容热容CV，m和摩尔等压热容Cp，m。
对一定量的物质系统，若以T、V作为独立变量，则热力学能的全微分dU可表示为
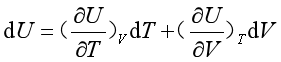
当体积不变时
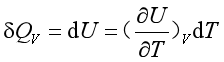
故等容热容可表示为
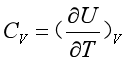（9a）
或等容时
（9b）
同理，若选择T，p作为焓的独立变量，则可得等压热容为
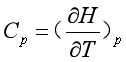（10a）
或等压时
（10b）
系统的热容是温度T的函数，具体的函数关系式，随物质聚集状态、温度范围的不同而异。由于Cp比CV更常用，在热力学数据手册中常收录物质的摩尔等压热容的两种经验式：
CP,m= a + bT + cT2 + … 或Cp,m= a + bT + c`T－2 + … （11）
式中a、b、c、c`各为经验常数，由物质的本性等决定，可通过实验测定求得，Cp，m的单位J·mol-1·K-1。
在等容下，定积分式（9b），可得
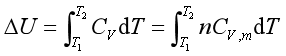（12）
在等压下，定积分式（10b），可得
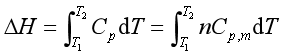（13）
应用式（12）和式（13）需注意，在温度变化范围里系统的物质仅发生单纯的状态变化、无相变和化学变化。
三、Cp与CV的关系
采用等压或等容的加热方式，加热一组成不变的均匀封闭系统，若升高相同的温度，则系统吸收的热是不同的。从式（10）可知，在等压、只作体积功的过程，系统吸收的热除有部分转化为系统的热力学能外，还有一部分热转化为反抗外压做的体积功，而等容过程吸收的热仅转化为系统的热力学能，所以一般情况下Cp与CV是不相等的。
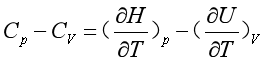
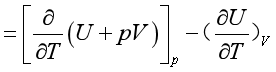
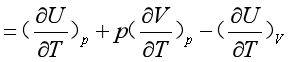（14）
设封闭系统的热力学能U =f(T.V), 其全微分
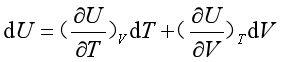
在等压p下，等式两边同除以dT ，得
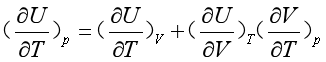（15）
式(13)代入式（12）,得
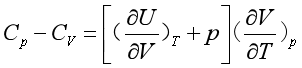（16a）
或 
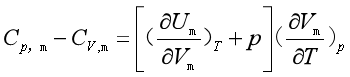（16b）
应当指出，式（14）（16a）、（16b）的关系适用任何封闭系统。
四、理想气体的热容
理想气体的热力学能U仅是温度的函数，所以
。理想气体的体积V =nRT/p，所以
。将这两个关系式代入式（16a）和（16b），分别可得
（17a）
或 
（17b）
根据气体分子运动论，对于单原子分子，除去其中电子与原子核内的能量外，可以认为它只具有平动运动，1mol单原子分子理想气体的热力学能为：
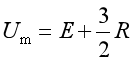
式中的E是1mol气体分子的电子和原子核内能量的总和，它不受温度的影响（核反应与热核反应除外），所以
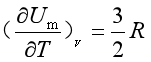(18 )
即单原子分子的理想气体，CV，m=(3/2)R ；若是线形多原子分子，还需考虑转动因素,CV，m，=(5/2)R；非线形多原子分子的CV，m=(6/2)R；说明理想气体的摩尔热容为常量,与温度无关。
在相当高的温度，双原子及多原子分子的CV，m要增大，这是因为它的分子中各原子间还有振动运动，这种振动运动能量是量子化的，其间能量差较大。在普通温度或低温时，大多数分子的振动运动都处于基态，只具有零点振动能，分子的振动运动被激发的机会较少（光化学或激光化学反应除外），此时振动运动对CV，m没有贡献。在相当高的温度时，分子的平均动能已相当大，分子间的碰撞足以使振动运动被激发到第一激发态或更高的激发态。温度愈高，这种激发的可能性愈大，其结果是分子的振动运动的平均能量随温度升高而不断增大。例如，H2(g)在不同温度时CV，m的实验值如下：
T/K 273 773 1273 1773 2273 2773
CV，m/J·K-1·mol-1 20.29 21.23 22.95 25.06 26.72 27.98
以上数据证实了上述的理论推测是合理的。
物质的等压热容与等容热容之比Cp/CV是一个重要的物理量，称为热容比，以符号
表示：
= Cp/CV
显然，
也是温度的函数，随气体分子的复杂性而减小。理想气体的热容比为常量，单原子气体
＝1.67，双原子分子气体
＝1.40；叁原子分子气体
＝1.33。
五、相变过程的焓变
在自然现象、科学实验、生产实践中，经常会遇到含有两个相以上的多相系统。我们把系统内物理性质和化学性质均匀的部分称为相(phase)。相与相之间存在界面，原则上可用机械的方法将不同的相分离。系统中同一种物质在不同相之间的转化称为相变。我们把物质处于热力学平衡条件下发生的相变称为可逆相变，如液态水在标准大气压下，100℃时蒸发为水蒸气的过程等；而把物质处于亚稳状态或非平衡状态下发生的相变称为不可逆相变，如在标准大气压py下，过冷水的结冰过程等。
在此只讨论纯物质的相变过程。常见的相变过程有熔化(fusion)、蒸发(evaporation)、升华(sublimation)、晶形转化（crystal transition）四种过程：
；
；
；
相变过程的摩尔熔化焓、摩尔蒸发焓、摩尔升华焓及摩尔转变焓可分别以ΔfusHm、ΔvapHm、ΔsubHm及ΔtrsHm表示。通常可在有关手册上查到常见物质在正常状态下（标准大气压力、相变温度时）的摩尔相变焓。在讨论相变焓时需注意相变进行的方向，如在相平衡温度和平衡压力下，物质的摩尔凝固焓
，摩尔凝结焓
，摩尔凝华焓
。
在恒温、恒压下，若系统进行的蒸发或升华相变过程发生在远离临界温度，液体或固体的体积与蒸发或升华后气体的体积相比可以忽略，即体积变化△V可近似视为等于气体的体积Vg，若气体遵循理想气体行为，则功
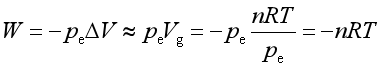
热力学能变为
ΔU =ΔH－Δ(pV) ≈ΔH－pVg≈ΔH－nRT
或ΔU = Qp+ W≈ΔH－nRT
所以，Qp=ΔH, 即相变过程的恒压热在量值上等于相变焓。
纯物质熔化和晶型转变是凝聚态之间的相变化过程，此过程系统体积的变化很小，体积功的数值W = －pΔV ≈0，Qp≈ΔU ，ΔU≈ΔH。所以，恒温恒压下，纯物质凝聚态之间相变过程的恒压热等于热力学能变及相变焓。
物质的相变焓是温度和压力的函数。与温度相比，压力对相变焓的影响较小，在通常情况下可以忽略。在较精确的计算中，需考虑相变焓与温度的关系。若相变过程在非恒压下进行，需注意此时Qp≠ΔH。
例3 已知在100℃和标准大气压下
，1kg水完全变成水蒸气需吸热2246.8kJ。试计算在标准大气压下，110 ℃的过热的水蒸发为同温度的水蒸气需要吸热多少？已知水蒸气和水的等压比热容分别为1.866kJ·kg-1·K-1和4.184 kJ·kg-1·K-1。
解 恒温、恒压下，过热水蒸发为水蒸气是不可逆相变过程。过热水蒸发所吸的热不易测定，但蒸发是在恒压条件下进行的，
，故可设计如下的途径，分三步来实现此变化，并求过程的焓变。
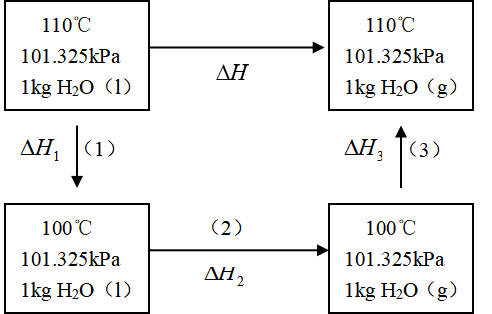
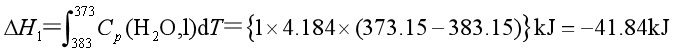
根据状态函数的性质，有
例4 在373.15K、标准大气压下，将0.056mol水蒸气恒温恒压压缩至体积为10－3m3的水蒸气，求该过程的Q、W、
、
。已知水的摩尔蒸发焓为40.66kJ·mol-1，水和水蒸汽的密度分别为10－3kg·m-3和0.6 kg·m-3。
解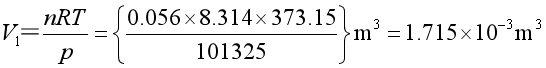 
在压缩过程必然有部分水蒸气凝结为水，由水蒸气的始态体积V1、终态体积V2，求凝结成水的量为
相变热、热力学能变及相变焓分别为
请同学们继续学习
