一、等温过程

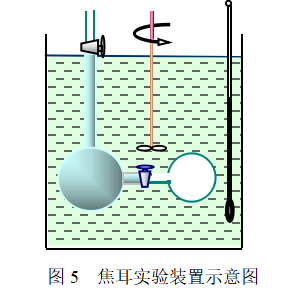
1843年焦耳设计了一个实验（如图5所示），将两个容量相等的容器浸在水浴中，两容器之间由带有活塞的管子连接起来，其中一个容器抽真空，另一个容器中装有一定温度和压力的气体，用精度为1/100的温度计测量实验过程水浴温度的变化。

打开活塞，气体就由装满气体的容器自由膨胀到原先抽成真空的容器中去，最后系统达到平衡状态，这时并没有观察到水温的变化，这一实验结果表明：（1）系统（气体）与环境（水浴）间没有热量的交换，Q= 0。根据ΔU = Q + W ，气体在自由膨胀中热力学能不变。

对于简单系统，通常可在T , V , p 中任选两个独立变量，再加上物质的量n , 就可以确定系统的状态及状态函数，如热力学能可表示T、p、n的函数

U = f (T , p , n)

由于状态函数具有全微分的性质，对于简单封闭系统n为定值，通常简化为U = f (T ,p )，但仍应理解为U是n的函数，对封闭系统的微小变化

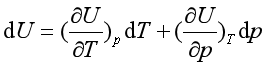(19 )

如果以U = f (T , V )表示，则：

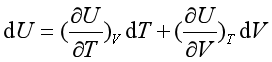(20)

根据式（20）讨论焦耳实验的结果：

因为                  dT = 0 和 dU = 0

所以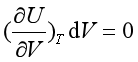                 

在焦耳实验中，气体的体积是增加的，即dV ＞0 , 所以

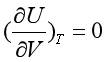（21a）

式（21a）表示在等温时，改变体积，气体的热力学能不变。同样还可证明：

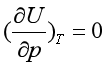 (21b)

式（21a）和（21b）都称为焦耳定律，它表明气体的热力学能仅仅是温度的函数，与体积、压力无关，即

  U = f (T) (22)

严格说，式（22）仅适用于理想气体，因为理想气体分子间无吸引力，分子本身没有体积，因此系统体积或压力的变化并不影响它的热力学能。用实际气体做实验时，由于水浴的热容量较大，即使气体膨胀需吸热，由于那时实验用的温度计只能测准至±0.01 ℃, 不可能测出气体温度的微小变化。由此可以认为，焦耳实验的结论应只适用于理想气体。

理想气体焓的变化为

ΔH = ΔU + Δ(pV) =ΔU + p₂V₂ - p₁V₁

在等温条件下，p₂V₂ ＝ p₁V₁ 及ΔU ＝ 0 ，所以ΔH = 0

又因为H = f (T , V)

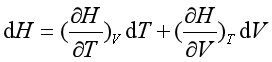
已证明等温条件下，dT = 0 , dH = 0 , 且又因为dV ≠ 0

所以 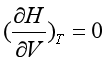                 （1.23a）

同理还可证明 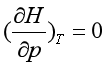         （1.23b）

所以理想气体的焓也仅是温度的函数，即

H = f (T) （1.24）

从微观上看，对于一定量有确定组成的气体，在状态变化中，气体热力学能的变化是由气体分子的动能和分子间的势能变化引起的。气体温度的高低反映了系统内分子平均动能的大小。理想气体不存在分子间的作用力，在p、V、T变化中，其热力学能的改变只是反映了分子动能的改变。由此就不难理解，理想气体温度不变时，无论体积和压力如何改变，其热力学能不变。

二、绝热过程

1. 绝热可逆过程

若系统和环境间在变化过程中无热交换，即Q= 0 , 则W =ΔU，这意味着在绝热压缩过程中，若环境对系统做功，系统的热力学能将增加，系统的温度升高；反之，在绝热膨胀过程中，系统的热力学能将减少，系统的温度降低。理想气体在准静态绝热过程中p、V、T间的变化遵循一定的规律，以下推导这一规律。

由热力学第一定律

dU =δQ +δW =δQ – pdV        

所以 δQ ＝ CV dT + pdV (25a)     

由焓的定义 H = U + pV

微分可得 dH = dU + pdV + Vdp 

可整理为 Cp dT =δQ + Vdp或δQ ＝ C_pdT – Vdp (25b)

绝热过程，δQ ＝ 0，由(25a)和(25b)，分别可得

pdV ＝ －C_V dT (26a)

Vdp ＝ C_pdT (26b)

将式（27b）除以式（27a），整理可得

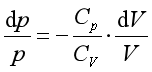
或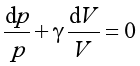(27)

式(27)为理想气体绝热可逆过程的微分方程。热容比虽然是温度的函数，但受温度的影响不大，故在温度变化不很大的范围内可视为常量，如CO₂从0℃变化到2000℃，从1.4变化到1.3。将式(27)进行不定积分，可得：

lnp + lnV = K

或 pV^γ =K₁(常量) （28a）

此式称为泊松方程。将理想气体状态方程式代入（29a）式，并作适当整理，可得

TV^γ-1 = K₂(常量) （28b）

P^1-γT^γ= K₃(常量) （28c）

式（28a）、（28b）、（28c）都称为理想气体绝热过程方程式，与理想气体pV = nRT这种表示某状态时p 、V 、 T关系的状态方程式不同，它们表明了理想气体绝热可逆过程中p 、V 、T间的关系，过程方程式的示意图如图6所示。

 

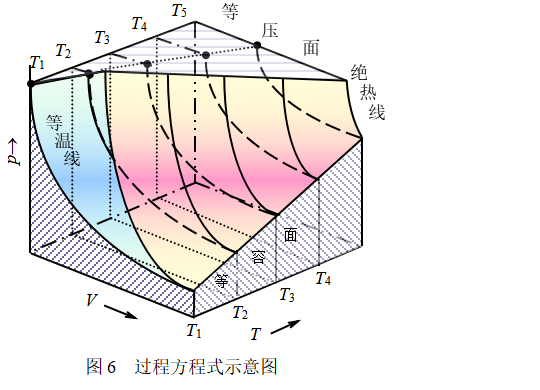
在以p、V 、T为三个互相垂直轴的坐标系里，根据理想气体的状态方程pV = nRT，可以构成一个曲面，曲面上的任一点，都符合理想气体状态方程式，因而可代表一个热力学状态，而曲面上的任一条曲线，则代表一个过程，见图6中的相关曲线分别表示：等温可逆过程以pV = K表示；绝热可逆过程以pV^γ ＝ K表示；等容可逆过程以p/T = K表示；等压可逆过程以V/T = K 表示，这四个等式中的常量K显然是不相等的。

根据p、V、T三者的关系，可以计算理想气体绝热可逆过程的功

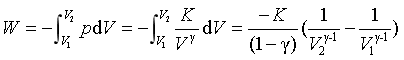
又因为                    p₁V₁^γ ＝ p₂V₂^γ ＝ K 

所以 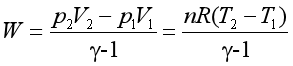                （29)

此外，理想气体绝热变化过程的功为

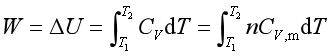
若视C_V，m 为常量，则

W = nCV，m (T₂ －T₁) (30)

由式(30)也可推得式(29)，所以，式(29)应适用于气体的绝热可逆和绝热不可逆过程。

2.绝热可逆与绝热不可逆过程的有关计算

例6  1摩尔理想气体，从始态27℃、1dm³, 经（1）绝热可逆膨胀，（2）绝热不可逆一步膨胀，均达到终态压力为101.325kPa ，分别求出两种过程终态的V和T，以及Q、W、ΔU和ΔH 。已知C_V,m = 12.55J·mol^-1·K^-1, C_p,m = 20.92 J·mol^-1·K^-1, γ= 1.67。

解（1）绝热可逆膨胀过程

系统的变化过程可表示如下：

1、终态T₂ 、V₂的计算

始态压力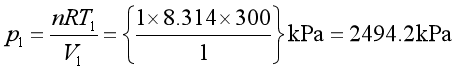  

由式（1.29a）p₁V₁^γ ＝ p₂V₂^γ，代入已知数据,

即       

解得              V₂ = 6.808dm³

所以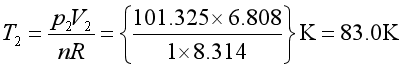              

2、热力学量的计算

绝热过程Q＝0，用式（31）计算过程的功

 

（2）绝热不可逆过程，反抗外压101.325kPa一步膨胀到终态

①终态T₂、V₂的计算

绝热过程，Q＝0，, 由关系式

和，可得

 

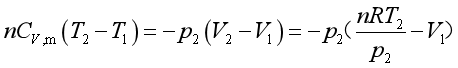
整理可得

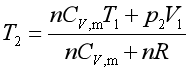
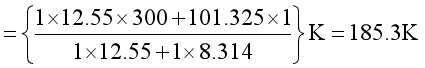
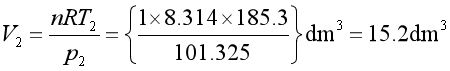
②、的计算：

绝热过程，Q＝0

计算结果表明，系统自同一始态出发，分别经绝热可逆和绝热不可逆过程，是不能到达同一终态的。

3. 绝热可逆与等温可逆过程比较

两过程的状态变化如图7所示：

状态Ⅰ→状态Ⅱ是等温可逆过程，曲线的斜率为

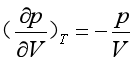(31a)

而状态Ⅰ→状态Ⅱ′是绝热可逆过程，曲线的斜率为

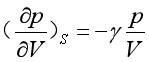(31b)

比较上述式(31a)和(31b)，由于热容比>1, 所以绝热可逆过程曲线的斜率较大，意味着系统从相同的始态出发，分别经等温可逆和绝热可逆过程，不能到达相同的终态。可以这样来理解：在等温膨胀时，只有体积膨胀一个因素导致压力降低；而在绝热膨胀时，由于系统不能从外界吸收热，只能依靠降低自身的热力学能来对抗外压p_e做功，所以体积膨胀和温度降低两个因素同时导致系统压力的降低，若指定两过程终态的压力相同，则终态温度必然不同。

三、理想气体的卡诺循环

在以上讨论关于理想气体各种状态变化过程的基础上，现讨论热力学基本循环—卡诺循环。卡诺于1824年设计了下列四个可逆步骤构成的循环：（1）恒温膨胀由AB；（2）绝热膨胀由BC；（3）恒温压缩由CD；（4）绝热压缩由DA；如图8所示。

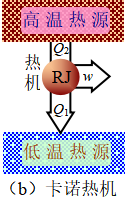
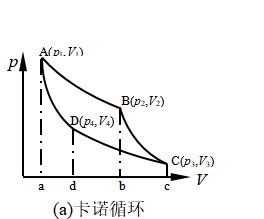
图8 卡诺循环和卡诺热机

众所周知，热机的是借助于系统经过由一系列步骤组成的循环过程，不断地从高温热源T₂吸收热Q₂，将其中一部分热转化为功，另一部分热Q₁放给低温热源T₁。热机的每一次循环，工作物质的状态变化在p -V 图上呈现一个闭合曲线。假定在热机的循环过程中，热源的热容很大，当系统与热源发生热交换时，热源的温度可始终保持不变。由卡诺循环构成的热机是理想的热机，通常称为卡诺热机。

现在计算卡诺循环过程每一步的热和功，设参与循环的工作物质为n mol理想气体。

（1）恒温可逆膨胀过程

系统与高温热源（T₂）接触，状态发生A(p₁,V₁,T₂) B(p₂,V₂,T₂)的变化。此为理想气体恒温过程，所以△U ＝0。此过程中，系统从温度为T₂的高温热源吸收热Q₂并将其全部转化为功

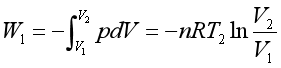
W₁在p -V图上等于曲线AB下面的面积S_ABba。

（2）绝热可逆膨胀过程

系统状态由B(p₂,V₂,T₂)C(p₃,V₃,T₁)，由于，所以系统消耗自身的热力学能对外作功，系统温度由T₂降至T₁，所做的功为

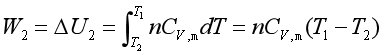
W₂相当于曲线BC下面的面积S_BCcb。

(3)恒温可逆压缩过程

系统于与另一低温热源T₁相接触，状态发生C(p₃,V₃,T₁)D(p₄,V₄,T₁)的变化。此为理想气体恒温压缩过程，△U₃ ＝0。系统所得功，全部转化为热Q₁并传给温度T₁的低温热源，压缩功W₃相当于曲线CD下面的面积S_CDdc。   

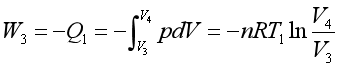
（4）绝热可逆压缩过程

系统状态从D(p₄,V₄,T₁)A(p₁,V₁,T₂)恢复原状。由于，系统所得的功全部转化为系统的热力学能，使系统的温度由T₁升至T₂。环境所做的功为

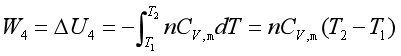
压缩功W₄相当于曲线DA下的面积S_DAad。

以上四个过程构成一个可逆循环，系统对环境所作的功相当于四边形ABCD所围成的面积，循环一周后系统恢复原状，则△U ＝0，所以

式中W是经一个循环后，系统所作的总功

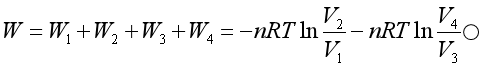
即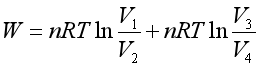  

由于过程（2）和（4）是绝热可逆过程，理想气体绝热过程方程式分别为

两式相除得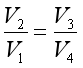

所以理想气体在一个卡诺循环过程所作的功为

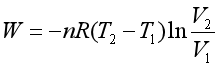
在整个卡诺循环过程中，系统从环境所吸收的热为

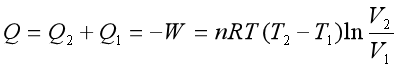
因为和，所以W＜0和Q＞0，表明卡诺循环过程是系统从高温热源吸收热，对环境作功。

热机在循环过程中所作的功与它从高温热源所吸收的热的比值称为热机的转换系数，也称为热机效率，用符号表示：

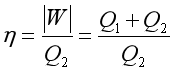
在上式中代入Q₁ 、Q₂，可得卡诺热机的热机效率为

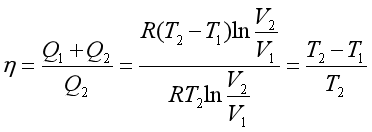
即 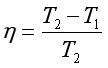（34）

从式（34）可知，可逆热机的效率只与两个热源的温度有关，两热源的温度差越大，热机效率越高，热的利用也越完全。例如，通常在工业上应用的蒸汽机的低温热源是大气，高温热源是高压过热蒸汽就是源于此理。可以通过理论证明：工作于相同温差热源条件下的所有热机中，可逆热机的效率最高，这就是著名的卡诺定理。应当指出，若卡诺热机中的工作物质不是理想气体，同样可以证明卡诺定理成立。