一、焦耳－汤姆逊效应

1852年，焦耳和汤姆逊设计了一个新的实验（如图9所示），比较精确地观察了气体通过一个绝热圆形筒中的多孔塞发生膨胀而引起的温度变化，所用的多孔塞起着阻碍气体畅流的作用，结果造成多孔塞两边的气流有一定的压力差。此实验可以证明：实际气体的热力学能和焓不仅是温度的函数，而且还与压力或体积有关，此因实际气体分子间存在相互作用力的缘故。

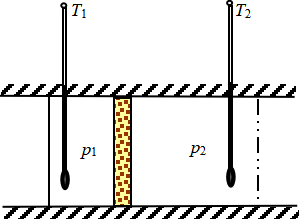
图9 焦耳-汤姆逊实验示意图

实验开始时，把压力p₁和温度T₁的实验气体连续地压过多孔塞产生膨胀，未达到稳定状态时，膨胀气流的温度不够稳定，此因绝热筒本身有一定的热容以及实验装置不可能完全绝热所致。只要维持通入气体的压力p₁和温度T₁，经多孔塞后气体的压力为p₂（p₁>p₂）, 连续进行一段时间后，系统能达到稳定的状态，出多孔塞气流的温度能稳定在T₂。实验结果发现，在室温附近，压力不很大的情况下，大多数气体如O₂、N₂、CO₂和空气等，通过多孔塞后温度降低，但H₂和He在通过多孔塞后温度却升高。例如0℃时，当压力差p₁－p₂＝1bar（10⁵Pa）时，O₂、N₂和空气的温度分别降低0.3℃左右，CO₂降低1.3 ℃，但是H₂却升高0.03 ℃。气体在一定的压力差下通过多孔塞进行绝热膨胀而发生温度变化的效应，称为焦耳－汤姆逊效应。若气体“变冷”（T₂<T₁），称为正焦耳－汤姆逊效应；若气体“变热”（T₂<T₁），称为负焦耳－汤姆逊效应。

在该过程中能量转换又是怎样的呢？为了简化起见，设在某时间内有一定量气体通过，该气体在p₁压力时的体积为V₁，这些气体在p₁压力下，被压过多孔塞，外压对气体作的功为－p₁ ，气体通过多孔塞反抗外压p₂，体积逐渐膨胀到V₂，此时气体作的功为，这样，外界对气体作的功为

整个过程是在绝热，即的情况下进行，根据热力学第一定律，此过程的

或                

移项后得          

即                ，

或                △H＝0

上式表明经上述膨胀后气体的焓不变。

我们将焦耳－汤姆逊实验中，气体稳定地从高压区流到低压区，而与周围介质没有热交换地过程，称为节流过程。显然，节流过程是一个复杂、不可逆、非平衡的等焓过程，气体通过小孔受到较大的阻力，在小孔处产生漩涡并有摩擦热产生等，气体的性质、起始温度、压力差（p₁—p₂）等都会影响过程中能量的转换。

节流过程在实际工作中经常遇到。例如，打开阀门后，气体由压缩机中逸出，蒸气轮机中蒸汽由喷嘴喷出等过程。工业上气体的液化与低温的获得，亦依赖于焦耳－汤姆逊效应的原理。下面进一步讨论气体的液化问题。

在节流过程中，多孔塞两边的压力差总是小于零，即。气体经多孔塞膨胀后“变冷”（T₂<T₁）或“变热”（T₂>T₁），将直接决定气体能否被液化。根据实验所测温度和压力的变化，可求得节流过程中温度对压力的变化率：

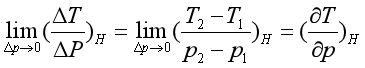
定义焦耳－汤姆逊系数为

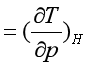_J-T  （36）

气体在节流过程压力降低，所以_J-T的正、负号取决于温度的变化。若_J-T＞0，则气体发生致冷效应；反之若_J-T＜0，则气体发生致热效应；若_J-T=0，则气体的温度无变化，我们将_J-T=0的温度称为转化温度。为何气体在不同的条件下_J-T的值可以大于零、小于零或等于零呢？

因为        

  

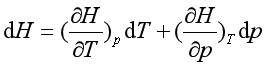
对节流过程，dH = 0，所以

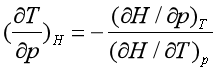
即              _J-T 

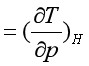
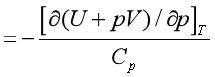
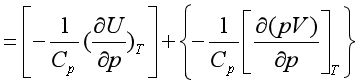（37） 

由式（37）可知，对于理想气体，因为

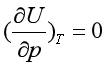及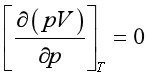

所以{_J-T}＝0，说明理想气体无焦耳-汤姆逊效应。实际气体的热力学能不仅是温度的函数，而且还与或有关。由于实际气体分子间有引力，在等温时当压力降低、气体发生膨胀时，必须从外界吸收能量以克服分子间的引力，这些能量使气体的热力学能增加，即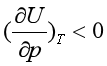。因此（37）式中，等式右边第一项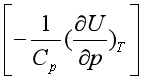总是大于零。对等式右边第二项，因为、，所以第二项的正、负号，分别取决于（pV）, 而（pV）的变化受实际气体分子间引力和气体分子的体积两个因素的影响。总之_J-T的正、负号取决于第一项和第二项的相对大小。

二、实际气体的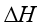和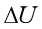

将实验测得_J-T，C_p及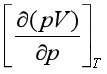代入式（37），可计算出实际气体的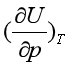。同时，又因

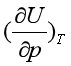
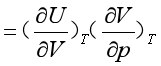
其中

（38）

式(38)中的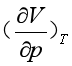，可由状态方程式求得或实验直接测定，最终可求出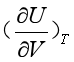。事实上，实际气体的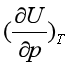和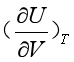均不等于零，说明实际气体的热力学能不仅与温度有关，还与压力或体积有关，即或。由于，焓也可以或表示。

通过热力学推导（参见第二章）可以得出：

    

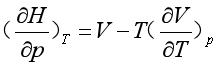
可见，由状态方程式可求出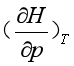，也可借助节流过程的_J-T及Cp等，直接计算实际气体的和。