热力学第一定律是能量守恒与转化定律在热力学系统中的应用。讨论热力学第一定律必须引进热力学的术语及热力学能、热、功、焓等重要概念，通过热力学第一定律在理想气体、实际气体及热化学反应中的应用，可以加深理解这些基本概念，熟练掌握热力学处理问题的特点和方法，并能灵活运用热力学原理、方法去解决实际问题。

一、基本内容

（一） 热力学术语

1.系统与环境

人们把物体群中所研究的对象划分出来，确定其范围和界限，这一作为研究对象的部分物体及其空间称为系统（或称体系）。环境是系统以外且与系统密切相关的物质及其所在的空间。系统与环境并无本质的差别，它们的划分是人为的，根据研究对象而选定；系统与环境间可以有实际界面存在，也可以没有实际界面存在；根据系统与环境间是否存在物质和能量的交换，系统又可以分为敞开系统、封闭系统与孤立（或隔离）系统。

2.状态与状态函数

系统里一切宏观性质的综合称为状态。描述系统状态的宏观物理量称为热力学性质或状态性质（状态变量），通常可用连续函数表示，依赖于其他状态变量的状态性质称状态函数。

系统的性质又称热力学变量，可分为广度性质（或称容量性质）和强度性质，广度性质与系统中物质的数量成正比，强度性质与系统物质的数量无关，取决于系统自身的特性。

3.过程和途径

系统发生状态的改变称为过程，它是指发生状态变化的方式，涉及为完成状态变化而经历一系列的中间状态和环境的作用。过程随条件的不同，可分为等温过程、等容过程、等焓过程、绝热过程、循环过程、多方过程、自由膨胀过程、相变过程等。完成过程的具体步骤称为途径。

(二) 热力学第一定律

热力学第一定律是涉及热现象领域内的能量守恒与转化定律。它有几种表述：①第一类永动机不可能制造成功；②孤立系统能量守恒；③系统经过绝热过程而发生状态改变，其所做功的大小与途径无关。

封闭系统的热力学第一定律可表示为，或，此式规定系统从环境吸热或接受外界的做功，过程的热和功均为正量值，若系统膨胀，功应为负量值。

1. 热力学能

热力学系统内部物质所有能量的总和，但不包括系统作为一个整体运动的动能和势能。

2. 热和功

热是系统与环境因温度差而交换或传递的能量，它是物质的大量微粒以无序运动的方式而传递的能量。除热量以外的其他各种形式传递的能量称为功，它以有序运动的形式表现出来。

热力学中讨论的功应包括体积功和非体积功。体积功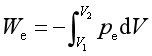。计算单纯变温过程的热量时，涉及系统改变单位温度时所吸收或放出的热，即系统的热容，由于系统处于不同的温度时，升高相同的温度所吸收的热量通常并不相同，因此，可以定义平均热容 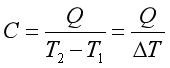，温度T时的热容则为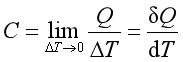。由于与过程有关，所以热容的量值也与过程有关。对于组成不变的均相封闭系统在等容或等压过程的热容，分别称为等容热容和等压热容，即
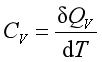      和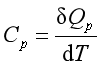        

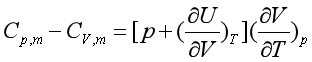对于1 mol物质，分别称为摩尔等容热容和摩尔等压热容。任何组成不变的均匀封闭系统。应用于理想气体，或。

3. 焓

焓是热力学的一个辅助函数，定义。焓不是能量函数，仅具有能量的量纲，它没有明确的物理意义。

由焓的定义式，等压过程，非等压过程。

（三）热力学第一定律的应用

应用于理想气体和实际气体涉及、、、的计算，因为是状态函数，和往往可通过设计一些中间过程去计算，只要始、终态确定，分别与原始条件相同，而和必须根据实际过程的条件进行计算。

焦耳实验表明理想气体的热力学能和焓仅是温度函数，即U= f（T），H= f（T）。

若系统没有相变和化学变化，仅发生温度的变化，则
 

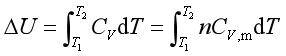
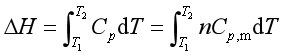
通常将和在一定温度范围内看作常量。事实上它们与温度有关，较常用的是，
或

理想气体绝热可逆与不可逆过程功的计算公式

或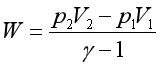

实际气体在焦耳-汤姆逊实验中（节流膨胀）的变化是一个等焓过程，定义焦耳-汤姆逊系数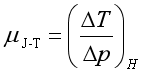。是温度、压力的函数，当＞0，气体发生致冷效应；＜0，气体发生致热效应。利用的正负可以判断实际气体能否液化。

（四）化学反应的焓变

在等温、等容或等温、等压下，不做非体积功的化学反应或某些物理化学过程中系统吸收或放出的热量等于过程的焓变。

化学反应的反应热除了与温度、压力有关外，还与反应进度有关，反应进度的定义为

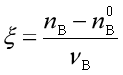       或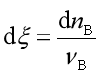            

在热化学中，常使用摩尔等压反应热与摩尔等容反应热，它们是指按反应计量式发生=1mol反应的等压反应热或等容反应热。两者之间的关系为

在热化学计算中常用到赫斯定律，即反应的焓变只与起反应的始、终态有关，而与变化的途径无关。

根据赫斯定律，用物质的标准摩尔生成焓数据计算反应的焓变的公式为 

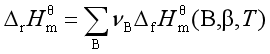
用物质的标准摩尔燃烧焓数据计算反应焓变的公式为

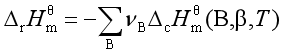
基尔霍夫定律是描述等压、不做非体积功和无相变时化学反应焓变与温度的关系。它的微分式为

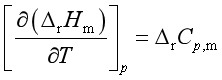
定积分式为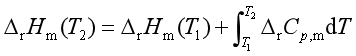         

若各物质均处于标准态，则

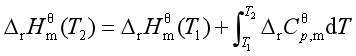
若物质的热容与温度有关，可将关系式代人上面积分式中，可求得一定压力下反应焓变与温度的关系式。

二、重点与难点

（一）正确理解状态函数的特性

①系统有确定的状态，状态函数就有确定的量值；

②系统的始，终态确定后，状态函数改变有确定的量值；

③系统恢复到原来状态，状态函数亦恢复到原量值。

需注意的是，一个指定的状态有确定的状态函数值，但是不同状态可以允许某一状态函数的量值相同。

（二）熟练掌握各种公式的适用条件与范围

善于区别易混淆的概念，从相互比较去加深对概念和公式的理解。例如：

①理想气体状态方程是描述状态参量间有的关系，而理想气体的过程是描述经某一过程参量间的关系，如理想气体绝热可逆过程

=常量，=常量，=常量

②节流过程与绝热过程的区别；节流过程与理想气体自由膨胀过程的区别。

③绝热可逆与绝热不可逆的区别。系统从同一始态出发经绝热可逆与绝热不可逆过程不能到达相同的终态。

④绝热燃烧反应放出的热量全部用于产物（包括剩余的反应物）的升温，所能达到的最高温度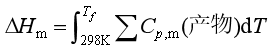，，该计算式与基尔霍夫积分式的意义完全不同，适用范围也不同。

（三） 可逆过程与不可逆过程的比较

可逆过程	不可逆过程
1.作用于系统的力无限小，即不平衡的力无限小，系统无限接近平衡态	1.作用于系统的力有确定的量值，不是无限小，系统至少有时处于非平衡态
2.过程的速率无限缓慢，所需时间无限长	2.过程的速率不是无限小
3.无任何摩擦阻力存在，无能量耗散	3.有阻力存在，有能量耗散
4.其逆过程能使系统与环境同时恢复原状	4.其逆过程不能使系统与环境同时恢复原状
5.实际不存在的理想过程	5.实际过程，但在某种情况下可使之接近于极限的可逆过程