第二章 热力学第二定律
知识点三：克劳修斯不等式与熵判据
一、可逆性判据
通过可逆与不可逆过程的热温商的讨论，定义了熵函数，并得到以下结果：对于可逆过程，存在关系式
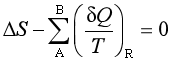
对于不可逆过程，则满足关系式
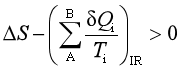
将此两项合并，即可以得到过程可逆性的判据：
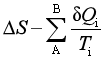≥0 （13）
“＝”表示过程可逆，“>”表示过程不可逆。式中ΔS为系统的熵变，δQ
是实际过程的热量，T
是环境的温度，在可逆过程中环境的温度等于系统的温度；ΔS与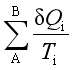
相差越大，
过程的不可逆程度就越大。此式称为克劳修斯不等式，也可作为热力学第二定律的数学表达式。
若变化无限微小，则得
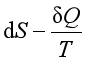≥0 （14）
或
≥
这是热力学第二定律的最普遍的表达式。本式所涉及的过程无限微小，而任何有限的过程都是由这些无限小的过程组成的。
对于绝热过程或隔离系统中进行的过程，则因系统与环境间没有热量交换，δQ＝0，所以
≥0 或
≥0 “＞”表示不可逆，“＝”表示可逆。由此可知，在绝热系统和隔离系统中，只有上述两种情况，不可能发生ΔS＜0的变化。
系统从某一始态出发，经绝热可逆过程，ΔS＝0，熵值不变，而经绝热不可逆过程，ΔS＞0，熵值增加。这说明，从同一始态出发，经绝热可逆过程与绝热不可逆过程不能达到同一终态，或者说在确定的两状态之间，不可能同时存在绝热可逆过程和绝热不可逆过程。
应该明确的是，利用克劳修斯不等式判断的是过程的可逆性，不论是自发变化还是非自发变化，过程是否可逆都由该方法进行判断。
二、方向性判据
对于隔离系统，系统与环境之间没有热和功的交换，环境对系统无任何干扰和影响，因此不会发生非自发变化，如果进行了不可逆过程，则必定是自发的。这就是说，在隔离系统中过程的可逆性与变化的方向性是一致的，也就是说隔离系统中不可逆过程的方向，就是自发变化的方向，因此便可以利用判断可逆性的方法来判断变化的方向性，即
ΔS隔离≥0
“＞”表示自发变化，“＝”表示达到平衡，这就是变化方向性的熵判据。它表明，在隔离系统中，若发生了自发变化，熵一定增加，系统达到平衡时，熵值已增到最大，不再改变。这一结论可表述为“一个隔离系统的熵永不减少”，这就是熵增加原理。
一般系统并非隔离系统，若进行了不可逆过程，则变化未必是自发变化，系统的熵也未必增加。所以应特别注意，用ΔS判断变化的方向性时，仅限于隔离系统。
三、总熵判据
系统的状态发生变化时，如果与热源交换了热量，则系统吸收或放出多少热，热源就放出或吸收等量的热，即
。如果热源的热容量很大，则与系统交换的热不足以引起其温度的改变，而且不论系统中进行的过程是否可逆，热源吸热或放热都可视为可逆进行，也就是说热源总是以等温可逆的方式与系统交换热量。
根据熵变的定义，可以求得热源的熵变为
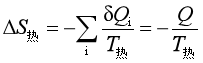（15）
式中Q为系统的热效应，
为热源温度。
回顾克劳修斯不等式（13）
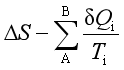≥0
式中ΔS是系统的熵变，可写成
；
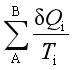是过程中的热温商之和，δQi是一微小过程中系统得失的热，Ti是热源的温度（即
），若
不变，则此不等式变为
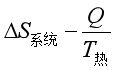≥0 根据式（15），上式中的第二项即热源的熵变，因而有
≥0 令
，则
≥0 可见，总熵变
≥0与克劳修斯不等式并无本质的区别，只是将过程中热温商的负值考虑为热源的熵变。所以，总熵变的作用与克劳修斯不等式的作用完全相同，可以作为过程可逆性的判据，“＞”表示不可逆，“＝”表示可逆。
不论自发变化或非自发变化，凡是实际进行的过程总是不可逆的，故
必大于零。
我们已经讨论过，隔离系统中发生的不可逆过程，必然是自发的，所以隔离系统的熵变
可以作为变化方向性的判据。显然，如果
代表
，也可以用
来判断变化的方向性，问题是在什么情况下
＝
。通常只有如下三种情况：1.若环境只是热源，则系统和环境之间仅存在热交换；2.存在系统对环境作功；以上二种情况热源的熵变就是环境的熵变，
，也就是隔离系统的熵变
。此时，总熵变可同时用于判断过程的可逆性和变化的方向性。3.若环境不只是热源，系统与环境除热交换外，同时存在环境对系统作功的情况，则
＞0便不能作为系统自发变化的判据，由于环境对系统做功，说明环境发生了一个自发变化，系统则是一个非自发变化，也就是由一个自发变化迫使一个非自发变化运作。此时
＞0只能说明一个非自发变化与自发变化的组合发生了一个自发的不可逆过程，但是却不能作为系统本身发生自发变化的判据。总之，作为变化方向性判据的先决条件是环境不对系统作功。因此，不能为了利用隔离系统的熵变来判断变化的方向性，而随意地把系统和环境作为一隔离系统处理。
请同学们继续学习
