熵变等于可逆过程中的热温商之和，这是计算各类过程熵变的出发点。对于可逆过程的熵变，可直接由热温商之和计算；对于不可逆过程的熵变，则应根据熵是状态函数，熵变值与途径无关的特性，在始、终态之间设计可逆过程来计算。

一、单纯pVT状态变化

1.等温过程

等温的状态变化过程，系统的熵变

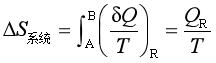
热源的熵变

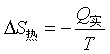
Q实为实际过程中系统的热效应。

若系统是理想气体，则等温过程中ΔU＝0，

于是

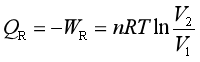
式中V₂和V₁分别是系统终态和始态的体积，由此得

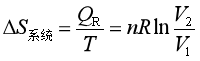（16）

例1 将2p^θ、11.2dm³的1mol理想气体，在273K，p^θ下膨胀至p^θ、22.4dm³，判断此过程是否可逆？

   

   

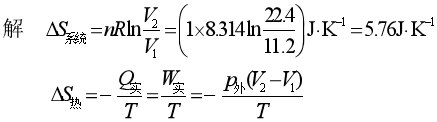
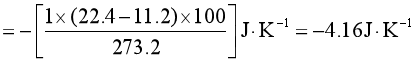
因＞0，所以该过程为不可逆过程。

2.恒压过程

系统经恒压过程，压力不变，但温度必将发生变化。此时系统的熵变应等于恒压下将系统可逆地从始态温度变到终态温度的熵变，即
     

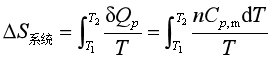（17）

若为常量，则     

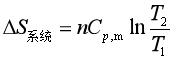（18）

该式适用于任何气、液、固体的恒压过程。

例2 NH₃（g）的＝(25.89+33.00×10^-3T/K-30.4×10-7T₂/K₂)J.K^-1.mol^-1。求1molNH₃（g）在恒压下由25℃加热到125℃的ΔS。

解   ΔS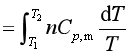

      
        
       

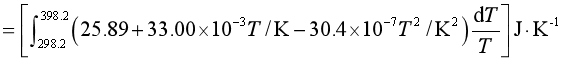
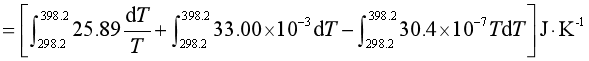
3.恒容过程         

与恒压过程类似，只需将,m换成,m，即

为常量时

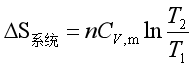（19）

例3 1mol的Ag在恒容条件下由0℃加热到30℃，求ΔS。已知在该温度区间Ag的为24.48。

4.理想气体任意状态变化过程

理想气体从状态A（p₁，V₁，T₁）变化到状态B（p₂，V₂，T₂），无论实际过程是否可逆，系统的熵变均可由至少两个不同的可逆过程求得。如图6所示

     

    

    

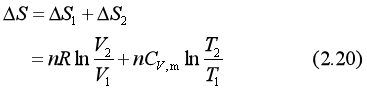
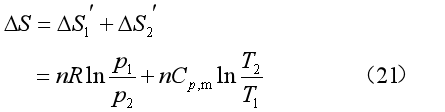
5.理想气体等温等压混合过程

设物质的量为的A气体与物质的量为的B气体分别置于一容器的两侧，用隔板隔离，它们的体积分别为V_A和V_B，温度为T，压力为p。抽去隔板后，两理想气体混合均匀，系统的T和p不变。如下图所示：

  

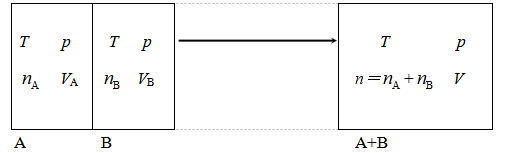
Δ_mixS＝ΔS_A+ΔS_B

对气体A而言，混合过程相当于等温下体积由V_A膨胀到V＝V_A+V_B，所以

同理，对于气体B而言，则有

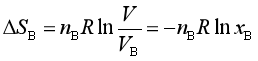
以上两式中、分别为A、B的摩尔分数。混合过程中系统的熵变为

Δ_mixS＝ΔS_A+ΔS_B
＝－n_ARlnx_A－n_BRlnx_B
＝－R（n_Alnx_A+n_Blnx_B）

因、均为小于1的正数，所以Δ_mixS必然大于零。在混合过程中，系统与热源之间未进行热的交换，所以。总熵变为

＞0

因为混合过程中，系统与环境之间毫无关系，所以这里的就表示隔离系统的熵变，而＞０，说明理想气体等温等压的混合过程是自发的不可逆过程。

对于多种理想气体等温等压下的混合过程，系统的混合熵变应为

（22）

二、相变化

1.可逆相变

可逆相变就是在相平衡温度、压力下进行的相变。因为过程等温可逆，相变热Q_p就是可逆热Q_R，所以

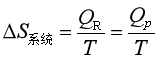
又因为相变中除去反抗外压作体积功之外，无其他功，所以Q_p＝ΔH，可逆相变热就是相变焓ΔH，则得

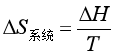（23）

热源的熵变应为

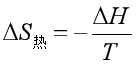
因此，系统熵变与热源熵变之和为零，即总熵变等于零。

例4 计算1mol冰在273.2K，下熔化为水的熵变。已知冰的熔化热为6004。

2.不可逆相变

不可逆相变是在非相平衡温度、压力下进行的相变。虽然过程是等温等压，相变热Q_p仍与相变焓ΔH相等，但它不是可逆热Q_R，所以ΔS≠ΔH/T，需要在变化的始、终态间设计一条可逆途径，通过一系列的可逆步骤来完成（其中包含可逆相变的步骤），由各可逆过程熵变的和计算出系统的熵变。设计过程的原则是不改变过程的压力，或不改变过程的温度。

例5  263.2K和的过冷水凝固为冰，求过程中的，及。

解

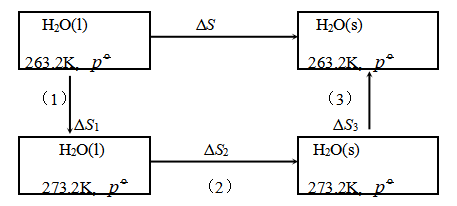
设计如上图所示的可逆途径来完成该不可逆相变：

（1）将263.2K的过冷水在下恒压可逆加热至273.2K和，其熵变为ΔS₁。

（2）在273.2K和下，将273.2K水恒温恒压可逆地凝固成273.2K冰，其熵变为ΔS₂。

（3）将273.2K和的冰恒压可逆冷却至263.2K和，其熵变为ΔS₃。

若已知液态水在273.2K时的凝固热为-6004；在题中温度范围内，水的=75.3，冰的=36.8，则可根据各可逆过程的特点分别计算熵变:

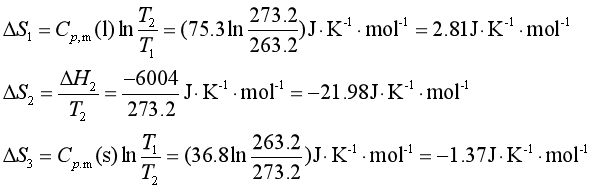
系统的熵变为

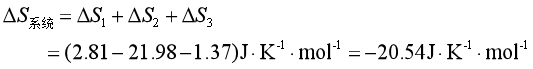
因冰在263.2K的熔化焓为5619，故过冷水在263.2K时凝固成冰的不可逆过程中，热源的熵变为

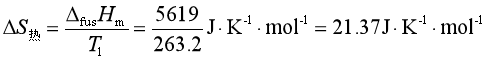
所以总熵变为

此即隔离系统的熵变，因其大于零，所以该过程为自发的不可逆过程。

三、化学变化

等温等压下的化学反应

aA+bB→yY+zZ

若能可逆进行，且知可逆热Q_R，则

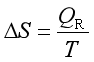
但是，除非作出特殊安排，化学反应通常都是不可逆过程，等温等压下的反应热是Q_p（＝Δ_rH_m），而不是Q_R。为得到可逆热Q_R，可将该反应安排成可逆电池，在电流趋近于零的条件下，让该反应在两电极上可逆地进行。此时，反应除了体积功外，还作出电功W_R′,W_R′＝-zEF。E是可逆电池的电动势，F为法拉第常量，F=96500，z是电池中进行单位反应进度时得失电子的物质的量。

根据热力学第一定律，反应等温等压不可逆进行时

Δ_rU_m=Q_p－p_eΔ_rV_m

等温等压在可逆电池中进行时

Δ_rU_m =Q_R－p_eΔ_rV_m+W_R′

以上两式中的Δ_rU_m同是该化学反应的热力学能变化，所以可得：

Q_R=Q_p－W_R′

即由化学反应的等压热及其可逆电功可以求得该反应的可逆热。

应注意的是，并非所有的化学反应都能安排成可逆电池，所以上述方法不具有普遍意义。关于反应能否安排成电池将在本书第九章中讨论。

若已知反应在T′、p时的ΔS′，则可根据S是状态函数的性质，按如下的思路求得T、p时的。设系统从始态经如下三个步骤到达终态：

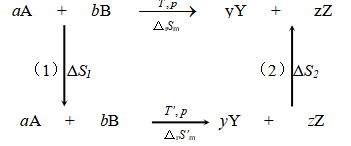
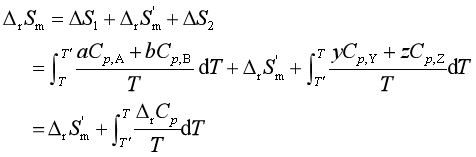
利用上式进行计算时，若在T和T′间出现物质的相态变化，还应计算（1）、（3）步骤中由相变引起的相变熵。

本法在计算化学反应的Δ_rS_m时，必须先知道反应在另一温度时的熵变，因此并未从根本上解决反应熵变的计算问题。若能求得各物质的熵值，便可以彻底解决化学反应熵变的计算，这将在热力学第三定律中讨论。

例6 在298K和下，反应H₂（g）+O₂（g）→H₂O（l）放热：285.83kJ·mol^-1，若反应在可逆电池中进行，则放热48.65kJ·mol^-1。求，和。

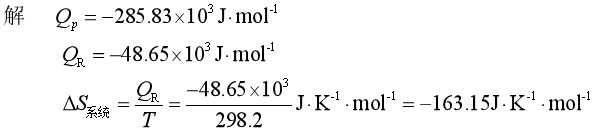
反应系统不可逆放热Q_p=－285.83kJ，但对于无限大热源来说是可逆地吸热285.83kJ，故

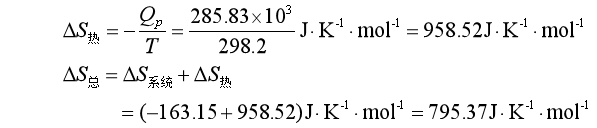
＞0，说明此反应是不可逆过程。