用熵增加原理来判断变化的方向性和限度，必须限于隔离系统，否则就会得出不合理的结论。但是很多变化通常是在等温等压或等温等容条件下进行，计算隔离系统的熵变时，必须考虑环境的熵变，这很不方便。若能像引进焓那样再引进新的状态函数，在某些特定的条件下，仅利用系统的这些函数值的变化就能判断自发变化的方向和限度，而不必再考虑环境的问题，这样就方便多了。为此亥姆霍兹和吉布斯又定义了两个热力学函数——亥姆霍兹自由能（A）和吉布斯自由能（G）。这两个状态函数与焓一样也是辅助函数，它们都不是热力学定律的直接结果。

一、亥姆霍兹自由能

设系统由温度为的热源吸收热量δQ，根据第二定律的数学表达式

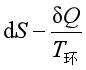≥0

将热力学第一定律δQ＝dU-δW代入上式可得             

-dU+dS≥-δW

δW包括体积功和非体积功。若系统的始态温度与终态温度都与不变的环境温度相等，即，则得

-d(U-TS)≥-δW（26）

令A≡U-TS        （27）

A称为亥姆霍兹自由能，又称功函，它是状态函数的组合，显然是系统的状态函数。由此可得

-dA≥-δW（28a）
-ΔA≥-W（28b）

“＝”表示可逆，“＜”表示不可逆。在等温可逆过程中，一封闭系统所作的功（-W_R）等于其功函的减少（-ΔA＝-W_R），等温不可逆过程中，一封闭系统所作的功（-W_IR）小于其功函的减少-ΔA（-ΔA>-W_IR）。

由于A是状态函数，ΔA的值只取决于系统的始、终两态，所以在等温条件下，可逆过程中系统所作的功（-W_R）大于它在不可逆过程中所作的功（-W_IR），即等温可逆过程系统作最大功。

A的物理意义只能在变化中加以理解，即：等温过程中，一封闭系统功函的变化等于系统所能作的最大功W_R。因A是状态函数，所以系统在其它过程中都具有功函的改变，但却不具有上述物理意义。

若在等温条件下，系统的体积不变，则不存在体积功，式（28）变为

-dA≥-δW′（29a）
-ΔA≥-W′（29b）

此式表示：在等温等容过程中，一封闭系统功函的减少－ΔA等于系统所能作的最大非体积功W_R′。

若在等温等容过程中不存在非体积功的交换（W′＝0），则式（29b）变为
 

ΔA≤0（30）

此式表示，在等温等容且不作非体积功的条件下，若ΔA＝0（功函值不变），过程为可逆；若ΔA<0（功函值减少），则过程不可逆。显然，在上述特定条件下，经可逆过程与不可逆过程不能达到同一状态。

二、吉布斯自由能

式（26）中的功是总功，若将总功分解为体积功与非体积功之和，则在等温条件下

-d(U-TS)≥- (δ+δ)

若系统始、终态压力相等并等于外压。即＝，则上式中δ＝，代入上式：

-d(U-TS)≥pdV-δW′

整理后可得

-d(U+pV-TS)≥-δW′

或

-d(H-TS)≥-δW′

令G≡H-TS        （31）

并称为吉布斯自由能，则得     

-dG≥-δW′（32a）

或

ΔG≥-W′（32b）

“＝”表示可逆，“＜”表示不可逆。在等温等压可逆过程中，一封闭系统所作的非体积功（-W_R′）等于其吉布斯自由能的减少（-ΔG＝-W_R′），等温等压下的不可逆过程中，一封闭系统所作的非体积功（-W_IR′）小于其吉布斯自由能的减少（-ΔG＞-W_IR′）。同样，由于G是状态函数，ΔG的值只取决于系统的始、终两态，所以在等温等压条件下，可逆过程中系统所作的非体积功（-W_R′）大于它在不可逆过程中所作的非体积功（-W_IR′），也就是在等温等压可逆过程中系统作最大的非体积功。

G的物理意义也只能在变化中加以理解，即：等温等压过程中，一封闭系统吉布斯自由能的变化等于系统所能作的最大非体积功。与A一样，对于其它过程，G有改变，但无明确的物理意义。

若系统在等温等压过程中不存在非体积功的交换（W′＝0），则               

ΔG≤0（33）

此式表示：在等温等压不作非体积功的条件下，若ΔG＝0（G值不变），过程可逆；若ΔG<0（G值减小），则过程不可逆。显然，在上述条件下，从同一始态出发，经可逆过程与不可逆过程不能达到同一状态。

到此为止，我们引进了两个新的状态函数——亥姆霍兹自由能（即功函）和吉布斯自由能，讨论了利用ΔA和ΔG来判断某些特定条件下过程的可逆性，但并没有涉及变化的方向性和平衡的条件。

三、变化的方向和平衡条件

由热力学第一、二定律的联合公式出发，引出了两个辅助的状态函数亥姆霍兹A自由能和吉布斯自由能G。联合公式中有关熵函数的不等式，推导出了功函和吉布斯自由能的不等式，由此可以判别变化的方向和平衡的条件。现将S、A及G的相关判据及限制条件归纳如下：

1.熵判据

对于隔离系统或绝热系统，dS≥0，“=”表示可逆，“＞”表示不可逆。在隔离系统中，如果发生了不可逆的变化，则必定是自发的。即在隔离系统中，自发变化总是朝向熵增加的方向进行，变化的结果是使系统趋向于平衡状态。系统达平衡状态后，其中的任何过程都是可逆的。所以判别变化方向性的熵判据应为：

≥0

“＞”表示变化自发，“=”表示平衡。

2.亥姆霍兹自由能判据

在等温、等容及不存在非体积功时，dA≥0，“=”表示可逆，“＞”表示不可逆。但在此条件下，系统处于无任何外来作用、任其自然的情况下，若发生不可逆过程，则必然为自发的变化。因此可以说在等温等容不作非体积功的条件下，自发变化总是向A减小的方向进行，直至A不变达到平衡。即亥姆霍兹A自由能判据可以写作：

（ΔA）_{T，V，W′=0}≤0　（34）

“＞”表示变化自发，“=”表示达到平衡。

3.吉布斯自由能判据

在等温等压不作其它功的条件下，dG≤0，“=”表示可逆，“＞”表示不可逆。同样，在此条件下，系统处于无任何外来作用、任其自然的情况下，若发生不可逆过程，则必然为自发的变化。因此，在等温等压不作非体积功的条件下，自发变化总是向吉布斯自由能减小的方向进行，直至其值不变达到平衡。即吉布斯自由能判据可以写作：

（ΔG）_{T，p，W′=0}≤0（35）

“＞”表示变化自发，“=”表示达到平衡。

以上各判据中，不等式可判别变化的方向，等式作为平衡的标志。应注意用熵判据时必须构成隔离系统，不仅要考虑系统自身的熵变，还应考虑热源的熵变。但用A和G来判别变化的方向性时，则只需考虑系统自身的性质。

实际上，上述亥姆霍兹A自由能和吉布斯自由能判据中W′=0的条件并不是必要的，以自由能判据为例简单说明如下：

在等温等压条件下，ΔG≤W′，或ΔG＝W_R′＜W_IR′。若ΔG ＞0，则W′＞0，说明系统消耗了环境的非体积功，其值至少等于W_R′，发生了非自发变化，即等温等压下吉布斯自由能增加的变化必为非自发变化。若ΔG＜0，则系统具有作功的能力，可利用来对外作非体积功，其值最大为|W_R′|，发生了自发变化。甚至在消耗非体积功的情况下，只要W′＜|ΔG|，系统仍具有作功的能力，发生自发变化。所以，通常情况下，只要满足等温等压条件，即可由（ΔG）_T，p≤0来判断变化的自发性。W′是否为零，一般不影响自发变化的方向。

与上面关于吉布斯自由能判据的讨论道理相同，等温等容条件下自发变化的方向和限度判据（即功函判据）为（ΔA）_T，V≤0。

这里只讨论了常用的等温等压和等温等容条件下变化方向和限度的判据，还可以得到等熵等容下的热力学能判据（ΔU_S，V≤0)和等熵等压下的焓判据(ΔH_S，p≤0)。这里不一一介绍，请读者自己考虑。

判断化学反应的方向性是非常重要的。例如，（ΔG)_T，p＜0，说明在等温等压下反应时，不但不需要消耗非体积功，相反地还可能提供非体积功。对于等温等压下的自发反应（ΔG＜0)，完全有可能在指定的温度和压力下自动进行；对于在等温等压下的非自发反应（ΔG＞0），在指定的温度和压力下必须消耗数值上至少等于ΔG的非体积功才有可能实现。

但热力学的判断只表明存在着一种可能性，并不意味着就可以实现，因为这里还有一个速率问题。热力学只能解决可能性，但如何把可能性转变为现实，则需要化学动力学来解决。