第二章 热力学第二定律
 知识点六:热力学函数间的关系式
知识点六:热力学函数间的关系式
在U、H、S、A和G五个热力学函数中,热力学能和熵是基本函数,应用较多的则是吉布斯自由能,熵具有特殊地位,用来判别变化方向性和过程可逆性的一些不等式最初就是从讨论熵函数开始的。在实际应用上述五个状态函数时,经常要与容易由实验测定的热力学函数P、V、T发生联系,为此,需要明确热力学函数之间的关系式,这些关系式可以由热力学第一定律和第二定律联合推导出来。
一、封闭系统的基本公式
U、H、S、A、G五个热力学函数之间有如下关系:
H=U+ pV
A=U-TS=H- pV-TS
G=H-TS=U+ pV-TS
对于组成不变的封闭系统,只存在体积功时,热力学第一定律的数学表达式为
dU=δQ-![]() dV
dV
第二定律的表达式为
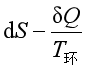 ≥0
≥0
合并以上两式,可得到δW′=0时的联合公式
dU≤![]() dS-
dS-![]() dV(36)
dV(36)
若过程可逆,则![]() ,
,![]() ,式(36)取等号,得
,式(36)取等号,得
dU=TdS-pdV(37)
根据H=U+ p V,微分后将式(37)代入,可得
dH=TdS+Vdp(38)
同样方法可得
dA=-SdT-pdV(39)
dG=-SdT+Vdp(40)
式(37)~(40)是由热力学一、二定律联合公式推得的,是四个最基本的公式,它们把平衡系统的八个热力学性质相互联系起来,并能推导出很多有用的关系式。这四个基本公式有时也被称为热力学基本方程式。
为了正确的运用以上四个基本公式,应特别注意它们的适用条件。在推导式(37)时,引进了三个条件:组成不变的封闭系统、δW′=0和可逆过程,应该说这三个条件就是使用四个基本公式的限制条件或适用范围。但是,由于U、H、S、A、G均为状态函数,它们的变化值只取决于始、终两态,与过程的可逆与否无关。所以,四个基本公式也同样适用于相同始、终态间的不可逆过程。但应当指明的是,若在封闭系统内发生不可逆的相变化或化学变化,则系统的组成就会发生不可逆的变化,因而不满足组成不变的前提条件,此时四个基本公式不能适用。若在封闭系统内发生可逆的相变化或化学变化,则组成变化是可逆的,可视为组成不变。所以四个基本公式仍然适用。
综上所述,四个基本公式的适用范围可以表述为:适用于组成不变的封闭系统,
δW′=0的可逆与不可逆过程。
四个基本公式中涉及到八个热力学函数,其中U与S和V相联系,称S、V为U的特征变量。同样,H的特征变量为S和p,A的特征变量为T和V,G的特征变量为T和p。当这四个热力学函数以相应的特征变量作为自变量时,它们就成为特性函数了。
二、对应系数关系式
将四个特性函数写成各自特征变量的全微分,并与四个基本公式相比较,便可得到四对关系式。
特性函数U=U(S、V)的全微分为
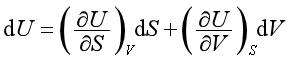
与基本公式
dU=TdS- pdV
相比较,可得
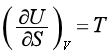
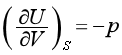 (41)
(41)
同理,由特性函数H=H(S,p)、A=A(T,V)、G=G(T,p)可以得到另外三组偏微商,即
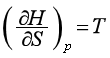
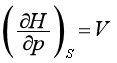 (42)
(42)
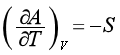
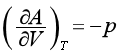 (43)
(43)
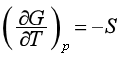
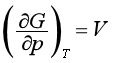 (44)
(44)
以上八个特性偏微商称为对应系数关系式。这些偏微商式也可由基本公式直接得到,例如:由dG=-SdT+Vdp,T一定时,dT=0,则得dG/dp=V,即可改写为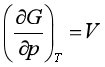
从对应系数关系式可知,若一容量性质对另一容量性质求导,得一强度性质(例如式41);若一容量性质对一强度性质求导,则得另一容量性质(例如式44)。
由对应系数关系式可以推论出特性函数随某一特征变量的变化趋势。例如由式(44)可以看出,由于系统的熵总是正值,所以在恒压下G将随着温度的升高而降低。而且系统的熵值越大,G受温度的影响越大;由于系统的体积总是正值,所以恒温下G将随压力的增大而增加,系统的体积越大,G受压力的影响也越大。
利用对应系数关系式,可计算在某些特定条件下特性函数的变化值。例如
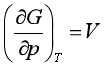 可得,等温过程中
可得,等温过程中
由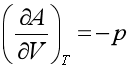 可得,等温过程中
可得,等温过程中
三、麦克斯韦关系式
利用全微分的性质,其二阶导数与求导次序无关,还可以得出另一组关系式。
例如对U的全微分式求导便有
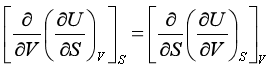
而 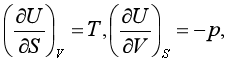 所以
所以
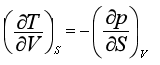 (45)
(45)
同理可得
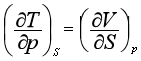 (46)
(46)
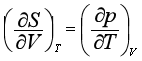 (47)
(47)
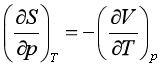 (48)
(48)
以上四个关系式称为麦克斯韦关系式。这些公式表示组成不变的封闭系统在平衡时的几个热力学函数之间的关系。根据这些关系式,可以用易于由实验测定的偏微商来代替那些不易直接测定的偏微商。
四、应用举例
1.热力学状态方程式
由基本公式dU=TdS-pdV,在定温下除以dV,得
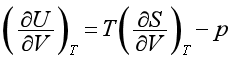
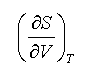 不易直接测定,但根据麦克斯韦关系式(2.47),上式可改写为
不易直接测定,但根据麦克斯韦关系式(2.47),上式可改写为 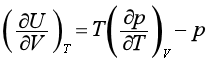 (49)
(49)
对于理想气体,p=nRT/V,则
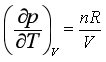
所以 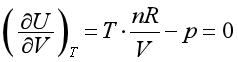
说明理想气体的热力学能与体积无关,由此从理论上证明了焦耳实验是热力学第一、第二定律的必然结果。
对于范德华气体,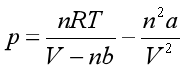 ,则
,则
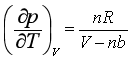
所以 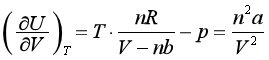
a为正值,故定温下范德华气体的热力学能随体积的增大而增加。分子间的相互作用越强,a值越大,体积对热力学能的影响也越大。
同理,由dH=TdS+Vdp可以得到
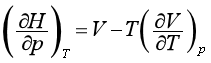 (50)
(50)
对于理想气体,必然得到
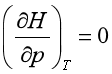
式(49)和式(50)称为热力学状态方程式,适用于不作非体积功的任何组成不变的封闭系统。
2.Cp与CV的关系
由热力学第一定律的关系式已经证得式(第一章16式)
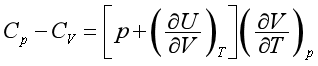
将热力学状态方程式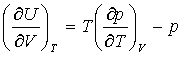 代入,得
代入,得
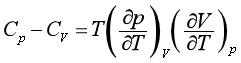 (51)
(51)
上式表明,从状态方程便可求得两种热容的差值。这是一个普遍的公式,适用于任何均相并且组成不变的系统。对于理想气体,对状态方程pV=nRT求导,即得
利用欧拉循环关系式:
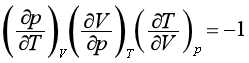
可得 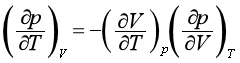
则式(51)可改写为更实用的形式:
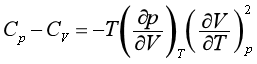
定义膨胀系数α和压缩系数β分别为
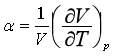
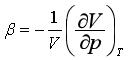
代入上式,得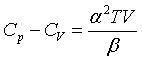
由该式可见,当T→0K时,Cp≈CV;因β总是正值,所以Cp≥CV;若α=0,则Cp=CV。液态水在101.325kPa,277.14K时,Vm达最小值,此时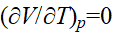 ,则α=0,所以水在101.325kPa,277.14K时,Cp=CV。
,则α=0,所以水在101.325kPa,277.14K时,Cp=CV。
3.定温下,CV与V的关系
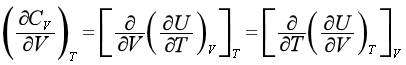
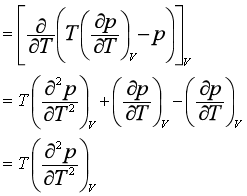
用同样方法可以得到