研究多组分系统热力学时，除了前面引入的热力学强度性质、容量性质外，还要引入两个新的概念——偏摩尔量与化学势。这是由于多组分系统由于组成改变引起的容量性质的改变并不与物质的量成正比例，例如，298.2K时纯水和纯乙醇的摩尔体积分别为18.09cm³， 58.35cm³，两者各取1mol混合后，其体积为74.43cm³ ，它小于（18.09+58.35）cm³，两者间的差值为2.010cm³。混合物的浓度不同时，体积差值也不同。体积如此，其它容量性质亦然（除质量外）。可见，在多组分系统中，要确定系统的状态，除了温度、压力外，还要指明系统的组成即指明每一种物质的数量，更重要的是，还要知道每一组分物质的量的改变所引起的系统容量性质的改变即偏摩尔量。

一、偏摩尔量的定义

设有一多组分均相系统，它由1，2，… k个组分组成，各组分的物质的量分别为,设某热力学容量性质(V、U、H、S、A、G)是，则

若温度、压力以及其组成发生微小改变，也随之改变，即

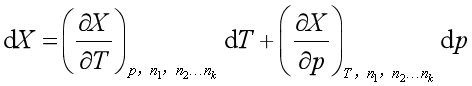
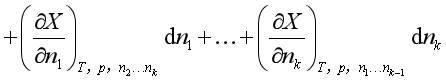
等温等压下，上式可简化为

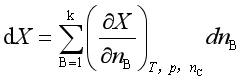（1）

上式中_C表示除B组分外，其余各组分的量均保持不变。

令               

 

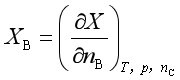（2）

得                

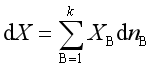（3）

就是物质B的某容量性质X的偏摩尔量

由式（1）可见，偏摩尔量的含义是在等温、等压除B组分外的其余组分物质的量不变的情况下，加入的物质B时引起的系统容量性质的改变。

由于偏摩尔量是个偏导数，因此偏摩尔量是强度性质，它可为正也可为负。在等温、等压、浓度不变的情况下，B组分的偏摩尔量在指定溶液中有确定的数值，在不同溶液中其偏摩尔量也不同。若浓度改变，也将改变。

对于纯物质，其偏摩尔量与摩尔量一致。

二、偏摩尔量的集合公式

一定温度和压力下，偏摩尔量与混合物的组成有关，若按照混合物组成同时向系统中加入微量的各组分形成混合物，因过程中组成恒定，偏摩尔量也不变。将式（3）积分，系统的容量性质X为

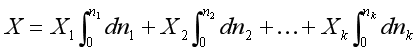
即                    

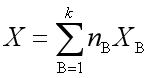（4）

式（4）称为偏摩尔量的集合公式。利用此式，可计算多组分系统的容量性质。由于系统有多种容量性质，故也有多种偏摩尔量，即
          

（5）

其中，偏摩尔吉布斯函数在实际应用中最重要。

对纯物质容量性质适用的热力学关系式，若用偏摩尔量代替相应的容量性质，一般情况下就可适用于多组分系统。如：

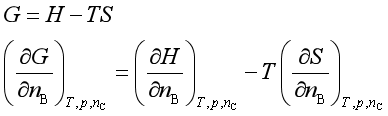
即                 

 

同样，可得           

等

例1  298.2K，101.325kPa时，物质的量为n的NaCl溶于1kg水中形成的溶液，其体积为，与物质的量n的关系为

计算n=0.1mol和0.5mol时的溶液中NaCl和水的偏摩尔体积。

解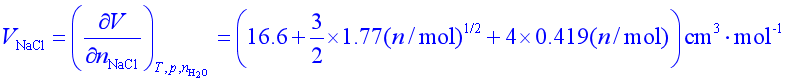  

时，

有所给关系式计算得  

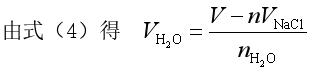
所以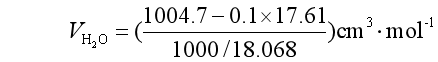

同法可求出n=0.5mol溶液中 ，
计算结果说明溶液浓度不同，组分的偏摩尔量是不同的。