第三章 多组分系统热力学
 知识点三:气体的化学势
知识点三:气体的化学势
一、理想气体的化学势
1.纯理想气体
对纯物质来说,
所以
恒温下
设气体压力为![]() 时,其化学势是
时,其化学势是![]() ,压力为p时的化学势为
,压力为p时的化学势为![]() 。当气体压力从
。当气体压力从![]() 变到P时,积分上式
变到P时,积分上式
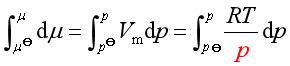
得
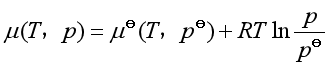 (11a)
(11a)
式中![]() 指的是温度为
指的是温度为![]() ,压力为
,压力为![]() 时纯理想气体的化学势,即理想气体标准态的化学势。因为它只与温度有关,故习惯上记作
时纯理想气体的化学势,即理想气体标准态的化学势。因为它只与温度有关,故习惯上记作![]() 。所以纯理想气体在温度为
。所以纯理想气体在温度为![]() 时化学势的表达式为
时化学势的表达式为
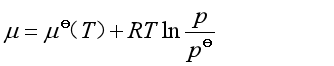 (11b)
(11b)
2. 理想气体混合物中任一组分的化学势
理想气体混合物的分子间作用力和分子体积均可忽略,其中每种气体的行为与该气体单独占有混合气体总体积时的行为相同。因此混合理想气体中B组分的化学势可使用它在纯态、压力为![]() 时的化学势表达式,即
时的化学势表达式,即
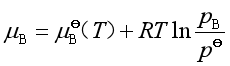 (12)
(12)
式中![]() 是B组分在混合气体中的分压,
是B组分在混合气体中的分压,![]() 是
是![]() 时组分B的化学势,故它是混合气体中B组分标准态的化学势。
时组分B的化学势,故它是混合气体中B组分标准态的化学势。
二、实际气体的化学势
1. 纯实际气体的化学势
纯实际气体的化学势就是其摩尔吉布斯函数,因此可以用![]() 求得,但由于每一种实际气体的状态方程不一样,因此
求得,但由于每一种实际气体的状态方程不一样,因此![]() 和
和![]() 的函数关系也不一样。故对每一种实际气体其化学势的表达式当然也不相同,这就给讨论问题带来了许多不便。为了使问题简化,路易斯提出实际气体化学势的表达式也沿用理想气体化学势表达式的形式,但引入一个校正因子,将实际气体对理想气体的偏差,都包含在校正因子内,从而使问题简化。
的函数关系也不一样。故对每一种实际气体其化学势的表达式当然也不相同,这就给讨论问题带来了许多不便。为了使问题简化,路易斯提出实际气体化学势的表达式也沿用理想气体化学势表达式的形式,但引入一个校正因子,将实际气体对理想气体的偏差,都包含在校正因子内,从而使问题简化。
据此,对压力为![]() 的纯实际气体其化学势
的纯实际气体其化学势
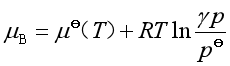 (13)
(13)
式中![]() 就是校正因子,令
就是校正因子,令
![]() (14)
(14)
![]() 称为逸度,
称为逸度,![]() 称为逸度因子。
称为逸度因子。
由此,在温度![]() 时,纯实际气体压力为
时,纯实际气体压力为![]() ,逸度为
,逸度为![]() 的化学势表达式为
的化学势表达式为
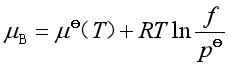 (15)
(15)
另有一理想气体设其压力为![]() ,在温度
,在温度![]() 时,其化学势为
时,其化学势为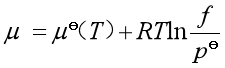 。可见,
。可见,![]() 可以理解为实际气体的修正后的压力,其单位与压力单位一致。
可以理解为实际气体的修正后的压力,其单位与压力单位一致。
因为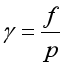 。若
。若![]() 与
与![]() 相差大,则
相差大,则![]() 偏离1越远,若
偏离1越远,若![]() 与
与![]() 相差小,
相差小,![]() 就接近于1。因此
就接近于1。因此![]() 偏离1的程度,说明实际气体偏离理想气体的程度。在极低压力下,实际气体可近似看作理想气体,此时
偏离1的程度,说明实际气体偏离理想气体的程度。在极低压力下,实际气体可近似看作理想气体,此时![]() =1。因此,
=1。因此,![]() 的定义为
的定义为
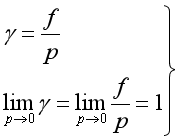 (16)
(16)
![]() 是量纲一的量。
是量纲一的量。
![]() :在式(15)中,当
:在式(15)中,当![]() 时,
时,![]() ,可见
,可见![]() 是逸度等于
是逸度等于![]() 时实际气体的化学势。因为在温度
时实际气体的化学势。因为在温度![]() 时,
时,![]() 的状态会有若干个,因此指定
的状态会有若干个,因此指定![]() 的状态为实际气体的标准态,故
的状态为实际气体的标准态,故![]() 就是实际气体在标准态(
就是实际气体在标准态(![]() ,
,![]() )时的化学势。显然,这是一个假想存在的状态,因为实际气体与理想气体存在偏差,才引入逸度概念,现在要
)时的化学势。显然,这是一个假想存在的状态,因为实际气体与理想气体存在偏差,才引入逸度概念,现在要![]() ,则一定是理想气体,所以该状态必为假想状态。
,则一定是理想气体,所以该状态必为假想状态。
由此可见,理想气体标准态的化学势与同温下实际气体标准态化学势是一致的,只是对理想气体而言,其标准态真实存在,对实际气体而言,其标准态是假想的状态。这样处理,对实际应用带来极大方便。例如,某气体从较低压![]() (此时可以理解为远小于
(此时可以理解为远小于![]() ,可视作理想气体)等温下变化至较高压力
,可视作理想气体)等温下变化至较高压力![]() 过程中,系统的吉布斯函数的变化值由于标准态选择一致,则
过程中,系统的吉布斯函数的变化值由于标准态选择一致,则![]() 可简单地表示出来。
可简单地表示出来。
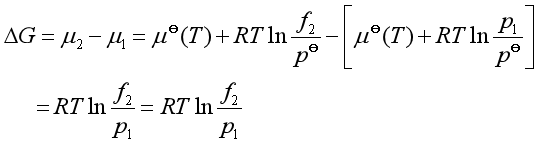
2. 实际气体混合物中各组分的化学势
实际气体混合物中任一组分B的化学势可用下式表达
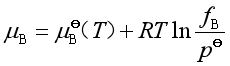 (17)
(17)
式中![]() 是B组分的逸度,它可以近似地用下式计算:
是B组分的逸度,它可以近似地用下式计算:
![]() (18)
(18)
式(18)称为路易斯—伦道尔规则。式中![]() 是B组分单独存在(纯B),并与混合气体具有相同温度,压力与混合气体总压一样时纯B的逸度。
是B组分单独存在(纯B),并与混合气体具有相同温度,压力与混合气体总压一样时纯B的逸度。![]() 是混合气体中B组分的摩尔分数。此规则可近似的使用到1000 kPa左右。
是混合气体中B组分的摩尔分数。此规则可近似的使用到1000 kPa左右。
3. 实际气体逸度因子的计算
求逸度实际上是求逸度因子,方法很多,现只介绍对比状态法。
对于理想气体 ![]()
对于实际气体,引入校正因子 ![]() , Z称为压缩因子
, Z称为压缩因子
故 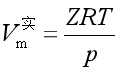
设![]() 是同温同压下理想气体的摩尔体积与实际气体的摩尔体积之差
是同温同压下理想气体的摩尔体积与实际气体的摩尔体积之差

两边积分,积分上下限分别是![]() 与
与![]() ,而
,而![]() 是极低压力,此时实际气体已经具有理想气体性质,故
是极低压力,此时实际气体已经具有理想气体性质,故![]() ,故得
,故得
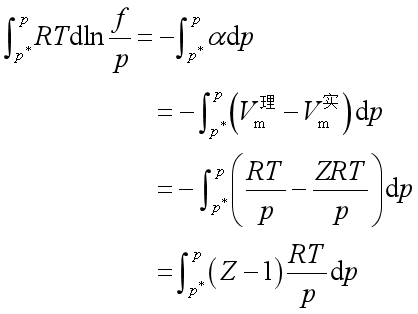
或 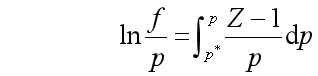
即 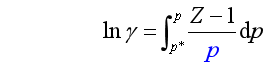 (19)
(19)
若知悉Z和p的关系,即可求![]() 。
。
对于实际气体,为求得压缩因子,通常引入对比温度τ,对比压力π,而Z就是π和τ的函数。![]()
定义
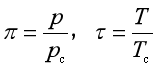
![]() 和
和![]() 分别称为临界压力和临界温度,每种气体的临界参数均可由物理化学数据手册上查到。实践证明,各种实际气体处于相同的π和相同的τ时,它们的逸度因子是相等的。式(19)可化成
分别称为临界压力和临界温度,每种气体的临界参数均可由物理化学数据手册上查到。实践证明,各种实际气体处于相同的π和相同的τ时,它们的逸度因子是相等的。式(19)可化成
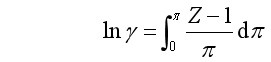 (20)
(20)
对某些气体实测π,τ,和![]() 后,作成牛顿图(图1),用此图可求得任一种气体的
后,作成牛顿图(图1),用此图可求得任一种气体的![]() 值。
值。
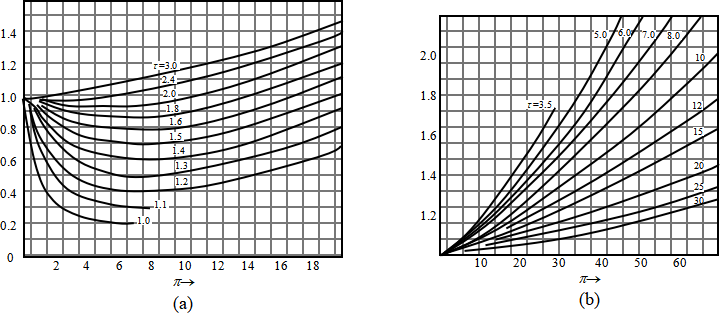
图1 牛顿图
