第三章 多组分系统热力学
 知识点四: 稀溶液的两个经验定律
知识点四: 稀溶液的两个经验定律
溶液的性质,除了与溶剂、溶质性质有关外,在很大程度上与溶液的浓度有关。一定温度下溶质在一定量的溶剂中的最大浓度,即饱和溶液的浓度,称为该温度下的溶解度。对于溶解度的大小,至今没有一个定量的公式进行计算,其值全靠实验确定。
把热力学的基本原理应用于溶液中,就形成了溶液热力学,溶液热力学的实验基础是下面的两条定律。
一、拉乌尔定律
很早以前人们就发现在一定温度下,当溶质溶于溶剂后,溶剂的蒸汽压会下降。1887年拉乌尔总结了这方面的规律,称为拉乌尔定律,可叙述为:“一定温度下,稀溶液中溶剂的蒸气压与溶液中溶剂的摩尔分数成正比,其比例系数就是同温度下纯溶剂的饱和蒸气压”。其数学表达式为:
![]() (21)
(21)
式中![]() 是溶液中溶剂的蒸气压,
是溶液中溶剂的蒸气压,![]() 是溶剂A的饱和蒸气压,
是溶剂A的饱和蒸气压,![]() 是溶液中溶剂的摩尔分数。
是溶液中溶剂的摩尔分数。
若溶液是二组分系统,则![]() ,所以式(21)可写为
,所以式(21)可写为
或
![]() (22)
(22)
在式(22)中,![]() 表示溶剂从纯态A变成溶液中A时蒸气压的下降值,所以式(22)说明溶剂蒸气压的下降与溶质的摩尔分数
表示溶剂从纯态A变成溶液中A时蒸气压的下降值,所以式(22)说明溶剂蒸气压的下降与溶质的摩尔分数![]() 成正比,其比例系数是同温下纯溶剂的饱和蒸气压。
成正比,其比例系数是同温下纯溶剂的饱和蒸气压。
拉乌尔定律是根据稀溶液的实验结果得出来的,所以对于大多数溶液来说,只有在低浓度范围内溶剂才遵守拉乌尔定律。因为只有在低浓度范围内,溶质分子很少,它与溶剂分子之间的作用可以忽略,因此溶剂分子所受的作用力与它在纯态时一样,仅仅由于单位体积溶剂分子数的减少而导致其蒸气压降低,故溶液中溶剂的蒸气压只与其摩尔分数成正比。当溶液浓度增加时,溶质分子对溶剂的作用就必须考虑,因此溶剂的蒸气压不仅与其摩尔分数有关,还与溶剂和溶质的性质有关,此时,拉乌尔定律就不再适用了。若溶剂与溶质结构相近,则溶剂分子与溶质分子间的作用力与纯溶剂分子间作用力几乎相等,拉乌尔定律就能在很大的浓度范围应用。
在使用拉乌尔定律时,应注意下面两点:
(1)拉乌尔定律适用于溶液已经达到平衡的系统,故溶液中溶剂的蒸气压就是平衡气相中溶剂组分的分压。
(2)若溶剂在溶液中发生缔合,缔合度不大时,拉乌尔定律仍可用,在计算溶剂的摩尔分数时,其摩尔质量按没缔合时计算,即按气态的摩尔质量算。
二、亨利定律
当溶质与溶剂形成溶液时,若溶质具有挥发性,或者溶质本身就是气体,溶质也有蒸气压。当气液平衡时,溶质在气相中的分压称为此温度下溶质的平衡分压。1903年,美国化学家亨利根据实验总结出对这种情况下的稀溶液适用的亨利定律,可叙述为:“一定温度下,在稀溶液中,一挥发性溶质的平衡分压与溶液中溶质的摩尔分数成正比”。
以![]() 表示等温下溶质的平衡分压,
表示等温下溶质的平衡分压,![]() 表示当溶液平衡时溶质在溶液中的摩尔分数,亨利定律的数学表达式为
表示当溶液平衡时溶质在溶液中的摩尔分数,亨利定律的数学表达式为
![]() (23a)
(23a)
式中![]() 称为亨利系数。它不是纯溶质B的饱和蒸气压
称为亨利系数。它不是纯溶质B的饱和蒸气压![]() ,
,![]() 既可大于
既可大于![]() ,也可小于
,也可小于![]() ,因为
,因为![]() 表示了溶剂与溶质之间的相互作用。
表示了溶剂与溶质之间的相互作用。
若将浓度很稀的溶质蒸气压与![]() 的直线关系外推到
的直线关系外推到![]() ,则纵坐标上的读数即为
,则纵坐标上的读数即为![]() 。可见,
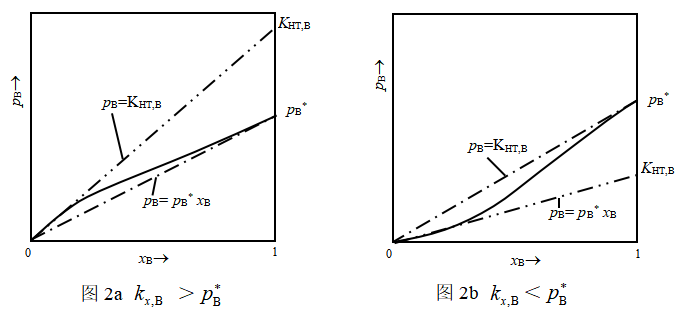
。可见,![]() 可看作是假想B在纯态时仍旧服从亨利定律时的饱和蒸气压(图2a和图2b),显然它们都不同于真正纯态B的饱和蒸气压
可看作是假想B在纯态时仍旧服从亨利定律时的饱和蒸气压(图2a和图2b),显然它们都不同于真正纯态B的饱和蒸气压![]() 。
。
亨利系数表示溶质汽化能力的大小,汽化能力大的溶质其![]() 也大,温度升高时,同种物质的
也大,温度升高时,同种物质的![]() 必增加。
必增加。
由于溶质在溶液中的浓度可分别用cB、mB、xB表示,故亨利定律还可表示为
![]() (23b)
(23b)
![]() (23c)
(23c)
其中![]() 也是亨利系数,
也是亨利系数,![]() 的单位为kPa·dm3·mol-1,
的单位为kPa·dm3·mol-1,![]() 的单位为kPa·kg·mol-1。
的单位为kPa·kg·mol-1。
在使用亨利定律时,溶质在气相和在溶液中的分子状态必须是相同的。若溶质在纯态时和在溶液中状态不同,如发生了缔合或解离,在计算溶质的浓度时,要按未缔合及未离解时计算。但若缔合度或离解度很大,亨利定律便不能使用。
亨利定律在生产、生活中应用很广,如啤酒厂装瓶时应用的压力应按亨利定律进行计算并考虑安全系数,以免使用过程中引起爆炸。在化工单元操作、传质理论中亨利定律也是重要理论依据。
例3 液体A和B形成理想液态混合物。现有一含A的摩尔分数为0.4的蒸气相,放在一个带活塞的气缸内,等温下将蒸气慢慢压缩。已知![]() 和
和![]() 分别为0.4
分别为0.4![]() 和1.2
和1.2![]() ,试计算:
,试计算:
(a)当液体开始凝聚出来时的蒸气总压。
(b)该液态混合物在正常沸点![]() 时的组成。
时的组成。
解 (a)液体刚好凝聚时呈现二相平衡,气相中的总压与液相组成的关系为:
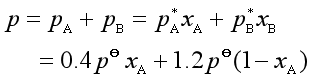
![]() (1)
(1)
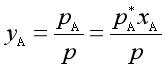
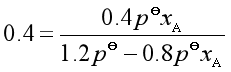
![]() (2)
(2)
将(2)式代入(1)式得
(b)正常沸点时:
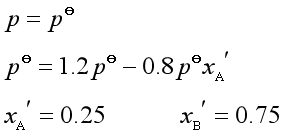
例4 合成氨的原料气通过水洗塔除去其中的CO2,已知气体混合物中含28%(体积)的CO2,水洗塔的操作压力为1.01×106Pa,温度为298K。计算每m3水最多可吸收多少CO2?(标准状况下体积)
已知298K时CO2在水中的![]() 。
。
解 由亨利定律得溶于水中的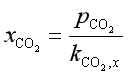
得
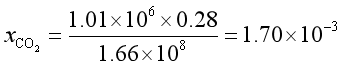
因为CO2在水中的浓度很小,故可认为是稀溶液,故
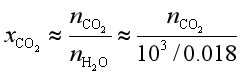
得到
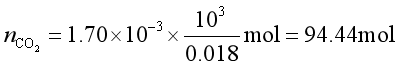
它在标准状况下的体积
有了热力学基本原理及上述两条实验定律,就可以讨论溶液所遵循的热力学基本规律。
