一、理想液态混合物的定义

一定温度下，液态混合物中的任一组分在全部组成范围内都服从拉乌尔定律，称作理想液态混合物。

各组分在整个浓度范围内都遵守拉乌尔定律，说明它们在构成液态混合物时，分子间作用力与在纯态时相同，因此混合后体积也不会发生改变，形成混合物时也无热效应，这就使处理问题简单化了。一些实际的液态混合物在一定的极限情况下也表现出相同的特性，进行适当处理后也可用类似的方法讨论。

由于电解质溶液中存在静电引力，故理想液态混合物这一概念仅适用于非电解质溶液。

二、理想液态混合物中任一组分的化学势表达式及标准态

由于液态混合物不区分溶质和溶剂，所以对于任一组分在热力学上的处理都是等同的，它们的化学势表达式形式相同，标准态也相同。

设在等温下有一液态混合物，不论其组分的挥发能力如何，都有各自的蒸气压，当气液两相平衡时，混合物中任一组分在两相中的化学势相等，即

（24）

设气体是理想气体混合物，则

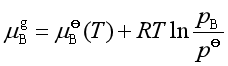
式中是气体中B组分的分压，也是液体中B组分的蒸气压

故                 

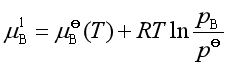（25）

这就是液态混合物中任一组分化学势的表达式。式（25）说明溶液中任一组分化学势可以用与它成平衡的气体的蒸气压的大小来衡量。

在得到式（25）时，未对液态混合物性质作任何限制，所以式（25）可适用于任何液态混合物中的任一组分。

对于理想液态混合物，由于每一个组分都服从拉乌尔定律，即

将上式代入式（25）中得

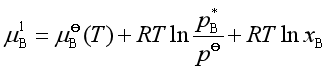（26）

等温等压下，式（26）右端前两项都是定值，因此可以合并成一项，即

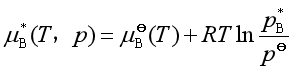（27）

将上式代入式（26）得   

（28）

式（28）只适用于理想液态混合物中的任一组分，此组分需满足：（1）服从拉乌尔定律；（2）蒸气当作理想气体的混合物。    

在式（28）中，当时，即纯液体B，，故是纯B液体在温度为，压力为时的化学势，它是一个真实存在的状态。由式（27）可知与直接相关，而是T、p的函数，所以也是，的函数。

按照规定，液态混合物中组分B的标准态是温度为T，压力为标准压力下的纯液体，即是理想液态混合物中任一组分标准态的化学势，它与不同，二者的的关系为

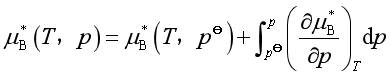
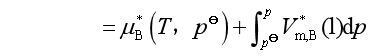（29）

式中是纯液体B的摩尔体积，也可以写作。

将式（29）代入式（28），得

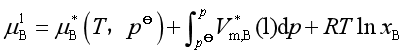（30）

由于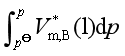值很小，故常常可以略去，式（30）可近似为

（31a）

或               

（31b）

是理想液态混合物中任一组分B标准态的化学势，这是一个真实存在的状态。
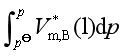式（28）与式（30）都是理想液态混合物中任一组分化学势的表达式，但应注意因与的差别，导致以上两式相差一项。而此项的数值很小，可以略去，故两个表达式近似相等，皆可使用，但应明确，标准态的化学势是，而非。

理想液态混合物中任一组分化学势的表达式，不仅指出了组分化学势与浓度的关系，同时它也是理想液态混合物的热力学定义式，即凡是混合物中各组分的化学势皆服从式（28），它就是理想液态混合物。

例5  298K，下若在：（a）大量等摩尔比的C₆H₆-C₆H₅CH₃液态混合物中；（b）1摩尔C₆H₆与1摩尔C₆H₅CH₃溶液中，这两种情况分离出1摩尔C₆H₆，求最少付给系统多少功？

解  在等温等压下，分离出1摩尔C₆H₆所需的最少功，即为此可逆过程所需的非体积功，此功等于该过程的
即                   

因此，只需要求得分离过程的即可。

（a）苯、甲苯性质近似，故它们的混合物可当作理想液态混合物。在二者分离时，各组分的状态发生改变。

初态              

末态            1mol纯苯         大量原溶液

由于甲苯在分离前后状态不变，故

所以

所以           

（b）由于系统仅由1摩尔C₆H₆与1摩尔C₆H₅CH₃组成，因此在此系统中分出1摩尔C₆H₆后，剩下的就是1摩尔纯C₆H₅CH₃了。
因此，初态         

 末态                     
所以  

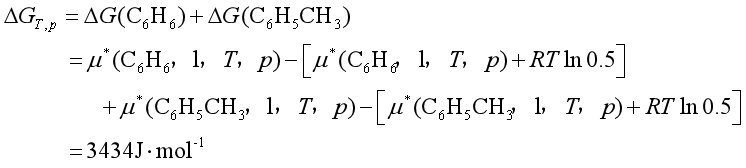
三、理想液态混合物的混合性质

1. 形成理想液态混合物时体积的改变

混合前各组分体积之和

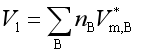
混合后系统体积

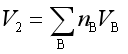
而

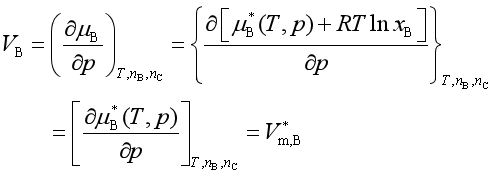
因各组分混合后之偏摩尔体积等于各组分纯态时的摩尔体积，故

（32）

形成理想液态混合物时，混合前后体积不发生改变。

2. 形成理想液态混合物时的焓变

混合前焓值          

混合后焓值          

因为                

所以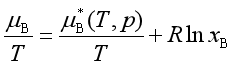             

上式对温度求导，得

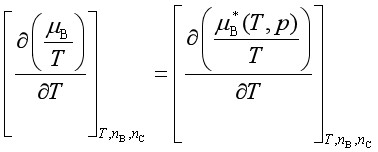
由吉布斯—亥姆霍兹方程可得

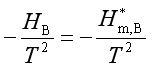
即                       

 

所以   

 

 （33）

故形成理想液态混合物时混合前后总焓没有变化，即混合热为0

3. 混合熵

混合前           

混合后           

因为            
              

即            

所以             （34）

由于恒＜1，故恒大于0。

4. 混合时吉布斯函数的改变

若形成液态混合物是在等温等压条件下，则

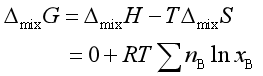
（3.35）

由于＜1，故恒小于0。

对于二元理想液态混合物，当时，是最高值，而是最低值，并且系统的总蒸气压与其组分浓度成直线关系，这些都可得到证明。

虽然理想液态混合物和理想气体一样，是一个极限的概念，提出理想液态混合物的概念使研究问题简化，但是与理想气体不同的是，非常类似理想液态混合物的系统实际存在。例如苯和甲苯系统，由于组分结构、性质都很近似，可以看作是理想液态混合物。另外，光学异构体，如左旋果糖和右旋葡萄糖组成的系统，同素异构物，如丙酸乙酯和乙酸丙酯所形成的液态混合物也可看作理想液体混合物。

例6  邻二甲苯和对二甲苯形成理想液态混合物，在25 ℃时，将1mol邻二甲苯与1mol对二甲苯混合，求此混合过程的Δ_mixV，Δ_mix H，Δ_mix S，Δ_mix G。

解   Δ_mix V=0；Δ_mix H=0

=（-8.314×2×1×ln0.5）J·K^-1         
       =11.5J·K^-1

=-3.43kJ