第四章 相平衡
 知识点一:相律
知识点一:相律
1873-1876年间,吉布斯研究了大量平衡系统,他凭借热力学导出了多相平衡系统的普遍规律--相律。
一、相、组分、自由度
研究相律,首先需要明确几个基本概念,即相、组分和自由度。
1.相
所谓相(Phase),就是系统中宏观物理性质和化学性质完全均匀一致的部分。例如:冰和含有固体NaCl的盐水系统(不考虑气相),其中大大小小的所有冰块为一相,过饱和下所有分散的固态盐粒为另一相,溶液又成单独第三相。相的数目称为相数,用符号“ ”表示。上述系统
”表示。上述系统 =3。对于一个指定的系统,不可光凭直观物理界面断定其
=3。对于一个指定的系统,不可光凭直观物理界面断定其 值,例如一盛水容器中间放有隔板,而系统的相数却仍为1,隔板并非相界面。一杯牛奶,看似一相,却是多相,因为借助于显微镜就会看到其中的油(相)和水(相)是完全不相溶的。新制备的氢氧化铁胶体,看似一相却是微多相。对于含有多种物质的系统,只有当这些物质以分子程度相互混合时(例如化合物,刚果红、蛋白质等高分子胶体,超导相),才是均相系统。
值,例如一盛水容器中间放有隔板,而系统的相数却仍为1,隔板并非相界面。一杯牛奶,看似一相,却是多相,因为借助于显微镜就会看到其中的油(相)和水(相)是完全不相溶的。新制备的氢氧化铁胶体,看似一相却是微多相。对于含有多种物质的系统,只有当这些物质以分子程度相互混合时(例如化合物,刚果红、蛋白质等高分子胶体,超导相),才是均相系统。
通常系统中成相的一般规律是:
(1)气体混合物为一相(高温、高压除外),完全互溶液体为一相。
(2)溶液视互溶程度的不同可根据分层情况形成多个平衡共存的液相。
(3)一种固体或固溶体便是一相,因此有几种固体及固溶体就有几个相。
(4)凡与系统平衡无关的因素,例如容器分隔、杂质含量不均等都不作为相数判断依据。
物质聚集状态的变化即所谓相变。例如,可用质量作用定律建立相变平衡常数表达式和组分在不同相间的质量分配定律;用等温方程式讨论组分浓度(活度)对相变方向的影响;利用有化学反应的相图进行反应的标准吉布斯函数变化和活度等相关的热力学量计算等等。
2. 组分
在平衡系统所处的条件下,能够确保各相组成所需的最少独立物种数称为独立组分数。用“K”表示。系统中的物种数用“S”表示。
组分数在规定范围内可以独立变化,而不会引起平衡系统相的数目与相的性质的改变。或者说,组分数确定后,系统才处于一定的平衡态。由于系统中存在着某些平衡关系,各物质间就可能有相互依存关系,通常只要选出某些关键性物质(即组分)来研究就够了。例如冰、水和水蒸气构成的平衡系统,三相中的物质都可用H2O表示,由此认定组分数为1,即使系统中存在水的缔合分子,还有H+、OH-等离子,但它们均与H2O存在化学平衡,离子与分子的浓度彼此依存,所以缔合分子与离子不是独立组分。
以任意量配制的NH4Cl(s),NH3(g)和HCl(g)的系统,系统中存在的化学物质种数称为物种数,用符号S表示。温度较高时,发生下列反应
NH4Cl(s) ![]() NH3(g)+HCl(g)
NH3(g)+HCl(g)
物种数S=3,但因化学平衡的存在,确定平衡系统中的各相组成所需最少的独立物质数应为K=S-R=3-1=2。通常以“R”标记系统中存在的独立的化学平衡数。
上述系统中,若使NH3(g)和HCl(g)的物质的量的比例为1:1,或者说这两种气体仅靠分解NH4Cl(s)所得,则在气相内这两种气体的物质的量相等,组成相同,确定一种物质的量,另一种物质的量也随之确定,因此系统又多了一个浓度限制条件。此时确保平衡系统中的各相组成所需最少的独立物质数为1,即K=1。今将除化学平衡外的其它独立浓度限制条件标记为R´,则组分数应是
K=S-R-R´ (1)
但需注意,只有同一相中的物种间可以考虑浓度限制条件。
系统中的物种数可随考虑问题的角度不同而变化,但组分数却是唯一不变的值。请读者 利用实际系统进行验证。诸如:
对于下列平衡系统
CaCO3(s)![]() CaO(s)+CO2(g)
CaO(s)+CO2(g)
 =3,独立组分数却为2。因为存在一个化学平衡(R=1),有一个化学势等式
=3,独立组分数却为2。因为存在一个化学平衡(R=1),有一个化学势等式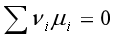 ,故上述的反应系统存在
,故上述的反应系统存在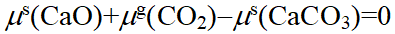 的关系,其中只有两种物质是独立的。该系统中的分解产物CaO(s)和CO2(g),尽管它们的物质的量相同,但CaO为纯固相,而CO2为气相, CaO(s)和CO2(g)间不存在浓度或分压关系,即R´=0,因此该系统的组分数
的关系,其中只有两种物质是独立的。该系统中的分解产物CaO(s)和CO2(g),尽管它们的物质的量相同,但CaO为纯固相,而CO2为气相, CaO(s)和CO2(g)间不存在浓度或分压关系,即R´=0,因此该系统的组分数
K=S-R-R´= 3-1-0 =2
若取CaO和CO2为起始物种,则可用CaO(s)+CO2(g)![]() CaCO3(s)表示CaCO3固相物种,同样,该平衡共存的三相系统的独立组分也可取CaCO3(s)和CaO(s)或CaCO3(s)和CO2(g)。
CaCO3(s)表示CaCO3固相物种,同样,该平衡共存的三相系统的独立组分也可取CaCO3(s)和CaO(s)或CaCO3(s)和CO2(g)。
3. 自由度
确定相平衡系统的状态所需的独立强度变量,称为系统的自由度(degree of freedom),如温度、压力或浓度等均可作为自由度。描述系统相平衡状态所需的最少强度性质数称为自由度数。另一种理解是在保持系统原有相的数目不变的相平衡状态下,系统所能最大限度改变的强度性质数称为自由度数。用“f”标记,自由度数等于零的系统,称为无变量系统,以此类推有单变量系统、双变量系统…。
例如水在298K及标准压力下,在一定范围内,我们可以任意地同时改变水的温度和压力,仍能保持水的液相存在,故称双变量系统,自由度数f=2。在p-T图中表现为一个平面区域。
又如水、水蒸气要保持在373K,标准压力下的两相共存,则系统为单变量f=1。因为若改变温度,同时又要保持原有两相并存,压力就要随之调整,反之亦然。这就是克劳修斯-克拉贝龙方程所表达的两相平衡的p=f(T)关系式,在p~T相图上描绘为曲线。
二、相律
一个包含着K种组分的平衡系统,设各组分分布在 个相中,对于每个相,便有温度、压力及(K-1)个物质的量分数(因
个相中,对于每个相,便有温度、压力及(K-1)个物质的量分数(因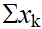 =1,故有一组分的x属于不言自明)这样一些强度性质,于是对每一相便有
=1,故有一组分的x属于不言自明)这样一些强度性质,于是对每一相便有
(K-1)+2=K+1
个强度性质,式中的2是指温度和压力。对于 个相,应有
个相,应有 (K+1)个强度性质,这是系统最大可能的总变量数。
但是一个多相平衡系统,必须满足:
(K+1)个强度性质,这是系统最大可能的总变量数。
但是一个多相平衡系统,必须满足:
1. 热平衡:各相间若非刚性绝热,各相温度必然相等,以保证各相之间无净热传递。
![]() ,共有(
,共有( -1)个等式
-1)个等式
2. 压力平衡:各相的压力必须相等,保证各相均无膨胀和收缩之虞。
![]() ,也共有(
,也共有( -1)个等式
-1)个等式
3. 相平衡:上述两点并非是相平衡的充分条件,K个组分能在两个相间成平衡的充分条件,必须使其在所有各相中的化学势相等,才能保证各相之间无物质的净转移(![]() ),于是便有
),于是便有
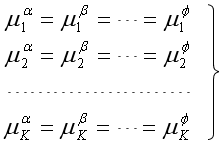 共有K(
共有K( -1)个等式
-1)个等式
这样,在一个相平衡系统的 (K+1)个强度性质的总数中便存在着上述3种平衡的限制,即变量间的关系式数目为
(K+1)个强度性质的总数中便存在着上述3种平衡的限制,即变量间的关系式数目为
( -1) +(
-1) +( -1)+K(
-1)+K( -1)(2)
-1)(2)
该相平衡系统的独立强度性质数则应为总变量数与变量间的关系式数之差,即
 (K+1)-[(
(K+1)-[( -1) +(
-1) +( -1)+K(
-1)+K( -1)]=K-
-1)]=K- +2
+2
此即相平衡系统的独立强度性质数,也即自由度数。因此
f =K - +2 (3)
+2 (3)
式 (3)就是吉布斯相律公式,它表示一定条件下,系统平衡共存的相数、组分数和自由度数之间的关系。其中的2是指温度和压力这两个变量。而在外压对相平衡系统影响不大的凝聚系统中,常看作定压,因此可将2改为1,称为条件自由度
f *= K- +1 (4)
+1 (4)
如果系统必须考虑其它因素(如电、磁、外力场等)的影响,则须以外因条件数“n”代替式(3)中的“2”,即
f = K- +n
+n
相律在相变热力学研究中发挥着重要的作用,它严格精确,无须知道分子的状态及微观变化,对于宏观系统普遍适用。但相律只能告诉我们总的方向,而不能确切地告诉我们具体是哪些相、哪些组分及哪些独立变量等具体问题。与热力学的其它结论一样,相律不能揭示过程发生的机理,不能告知达到平衡的时间;也不能预测诸如快冷、偏析等不平衡的相态。应用相律时首先应考察系统是否符合相律成立的条件,并确定组分数。
例1 指出下面二组分平衡系统中的相数、独立组分数和自由度数。
(1)部分互溶的两个液相成平衡。
(2)部分互溶的两个溶液与其蒸气成平衡。
(3)气态氢和氧在25℃与其水溶液呈平衡。
(4)气态氢、氧和水在高温、有催化剂存在。
解 (1) =2, K=2, f=K-
=2, K=2, f=K- +2=2,即压力、温度和浓度,其中有2个是自变量。
+2=2,即压力、温度和浓度,其中有2个是自变量。
(2) =3, K=2, f=K-
=3, K=2, f=K- +2=1。为确保平衡,温度、压力中只能有1个自变量。
+2=1。为确保平衡,温度、压力中只能有1个自变量。
(3) =2, K=3, f*=K-
=2, K=3, f*=K- +1=2。氢气分压、氧气分压与系统总压中有2个是自变量。
+1=2。氢气分压、氧气分压与系统总压中有2个是自变量。
(4) =2,增加1个氢、氧与水的化学平衡,R=1, K=S-R=2,f=K-
=2,增加1个氢、氧与水的化学平衡,R=1, K=S-R=2,f=K- +2=2。
+2=2。
例2 NaHCO3(s)在真空容器中部分分解为Na2CO3(s)、H2O(g)和CO2(g):
2NaHCO3(s)=NaCO3(s)十H2O(g)十CO2(g)
该系统的自由度数、组分数及相数各为多少?
解 有1个气相与2个固相, =3;存在化学平衡,R=1;同时,在物理平衡与化学平衡过程中,产物Na2CO3(s)、H2O(g)和CO2(g)间不存在浓度或分压依赖关系,所以R´=1,C=S-R-R´=4-1-1=2;f=2-3+2=1。
=3;存在化学平衡,R=1;同时,在物理平衡与化学平衡过程中,产物Na2CO3(s)、H2O(g)和CO2(g)间不存在浓度或分压依赖关系,所以R´=1,C=S-R-R´=4-1-1=2;f=2-3+2=1。
