第五章 化学平衡
 知识点二:化学反应的标准平衡常数
知识点二:化学反应的标准平衡常数
一、标准平衡常数的定义
对于无限大量的封闭系统中的任一化学反应,若反应是在等温等压条件下进行,则按式(4) 有
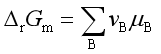
系统中B组分的化学势μB可表达为
![]() (5)
(5)
式中![]() 是B组分在温度
是B组分在温度![]() 的标准状态下的化学势,
的标准状态下的化学势,![]() 为B组分的活度。不同系统中,
为B组分的活度。不同系统中,![]() 和
和![]() 有不同的内涵。
有不同的内涵。
对气相反应, ![]() 是
是![]() 。
。![]() 为
为![]() 或
或![]()
对于液态混合物中的任一组分或溶液中的溶剂,![]() 是
是![]() ,即
,即![]() ,
,![]() 下纯液体B的化学势,
下纯液体B的化学势, ![]() 。
。
对于稀溶液中的溶质,![]() 和
和![]() 随溶质浓度的表示法不同而异。溶质浓度用
随溶质浓度的表示法不同而异。溶质浓度用![]() 表示,
表示,![]() 是
是![]() ,
,![]() 时假想液态纯溶质的化学势,
时假想液态纯溶质的化学势,![]() ;溶质浓度用
;溶质浓度用 ![]() 表示,
表示,![]() 是
是![]() ,
,![]() 时,
时,![]() =1mol·kg-1 且服从亨利定律的假想态的化学势,
=1mol·kg-1 且服从亨利定律的假想态的化学势, 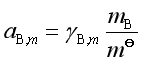 ;溶质浓度用
;溶质浓度用![]() 表示,
表示,![]() 是
是![]() ,
,![]() 时,
时, ![]() =1mol·dm-3 ,且服从亨利定律的假想态的化学势,
=1mol·dm-3 ,且服从亨利定律的假想态的化学势, 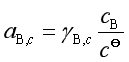 。
。
将式(5)代入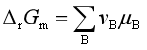 中,并统一用
中,并统一用![]() 表示
表示![]() ,则
,则
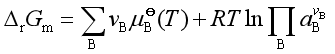 (6)
(6)
与式(4)对照可知,
![]() (7)
(7)
![]() 称为化学反应在温度
称为化学反应在温度![]() 时的标准摩尔反应吉布斯自由能。
时的标准摩尔反应吉布斯自由能。
将式(7)其代入(6),可得
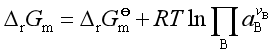 (8)
(8)
反应达平衡时![]() =0 ,
=0 ,![]() ,则
,则
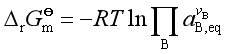 (9)
(9)
令 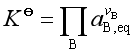 (10)
(10)
![]() 为反应达到平衡时参与反应的各物质的活度幂函数之积,代入式(9)得
为反应达到平衡时参与反应的各物质的活度幂函数之积,代入式(9)得
![]() (11)
(11)
或
![]() (12)
(12)
因![]() 与标准态化学势直接相关,所以称
与标准态化学势直接相关,所以称![]() 为标准平衡常数,式(12)为标准平衡常数的热力学定义式,它对任何化学反应都适用,只是各种反应系统
为标准平衡常数,式(12)为标准平衡常数的热力学定义式,它对任何化学反应都适用,只是各种反应系统![]() 的含义不同,所以
的含义不同,所以![]() 的意义也因系统而异,它与参与反应的各物质的本性、温度及标准态的选择有关。 对指定的反应,它只是温度的函数,为量纲一的量。
的意义也因系统而异,它与参与反应的各物质的本性、温度及标准态的选择有关。 对指定的反应,它只是温度的函数,为量纲一的量。
再令![]() =
=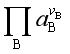 ,
, ![]() 为反应进度ξ时,参与反应的各物质的活度幂函数之积,常称其为活度商。
为反应进度ξ时,参与反应的各物质的活度幂函数之积,常称其为活度商。
将式(11)与![]() 代入(8),可得
代入(8),可得
![]() (13)
(13)
式(13)称为化学反应等温方程式。由该方程可知
若![]() >
>![]() , 则
, 则![]() <0,反应自动自左向右进行;
<0,反应自动自左向右进行;
若![]() <
<![]() , 则
, 则![]() >0,反应自动逆向进行;
>0,反应自动逆向进行;
若![]() =
=![]() , 则
, 则![]() =0,反应达到平衡。
=0,反应达到平衡。
可见,由任意状态的![]() 与标准平衡常数
与标准平衡常数![]() 的比较,即可由化学反应等温式判断反应的方向和限度。
的比较,即可由化学反应等温式判断反应的方向和限度。
化学反应等温方程式也可表示为
![]() (14)
(14)
由上式可见,已知温度T时的![]() 和各物质的活度,即可求得该温度下的摩尔反应吉布斯自由能
和各物质的活度,即可求得该温度下的摩尔反应吉布斯自由能![]() ,欲使反应进行,即
,欲使反应进行,即![]() <0,则在一定程度上可以通过调整
<0,则在一定程度上可以通过调整![]() 值来实现。应注意的是,必须用
值来实现。应注意的是,必须用![]() 判别反应进行的方向,而不能使用
判别反应进行的方向,而不能使用![]() 。但在
。但在![]() 值达到一定值时(大于40 kJ·mol-1或小于﹣40 kJ·mol-1),很难通过调整
值达到一定值时(大于40 kJ·mol-1或小于﹣40 kJ·mol-1),很难通过调整![]() 改变
改变![]() 的符号,此时可以用
的符号,此时可以用![]() 估计反应的可行性。
估计反应的可行性。
二、标准平衡常数与化学反应计量方程式的关系
因![]() 与化学反应中物质的计量数有关,所以由式
与化学反应中物质的计量数有关,所以由式![]() 可知,
可知, ![]() 必与化学反应计量方程式的写法有关:
必与化学反应计量方程式的写法有关:
例如:反应
(1) 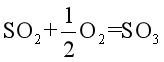
![]()
(2) ![]()
![]()
因 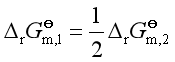
所以 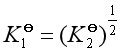
可见,对于同一化学反应,当计量方程式的计量数是倍数关系时,标准平衡常数是指数关系。同理,在相同温度下,若一个化学反应可以由几个不同的化学反应相加、减得到,则该化学反应的标准摩尔吉布斯自由能与各相关反应的标准摩尔吉布斯自由能是相加、减的关系,但标准平衡常数之间是相乘、除的关系。
