第五章 化学平衡
 知识点三:各种反应系统的平衡常数
知识点三:各种反应系统的平衡常数
一、气相反应的平衡常数
1. 理想气体化学反应
参与反应的任一理想气体组分的化学势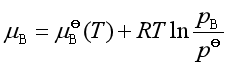
即 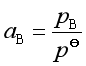
所以 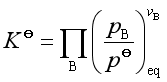 (15)
(15)
式(15)是理想气体反应标准平衡常数的表达式,它是一个只取决于温度和物质本性的量纲一的量。
除了![]() 外,在实际应用中,理想气体反应还常使用经验平衡常数
外,在实际应用中,理想气体反应还常使用经验平衡常数![]() ,
, ![]() 和
和![]() 。
。 ![]() 是以分压表示的平衡常数,定义
是以分压表示的平衡常数,定义
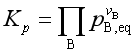 (16)
(16)
所以 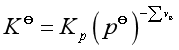 (17)
(17)
因为![]() 仅是温度的函数,故
仅是温度的函数,故![]() 也只是温度的函数。
也只是温度的函数。![]() 的单位是
的单位是![]() 。当
。当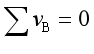 时,
时,![]() 与
与![]() 在量值上相等。
在量值上相等。
![]() 是以浓度表示的平衡常数,定义
是以浓度表示的平衡常数,定义
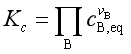 (18)
(18)
因 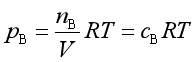
所以 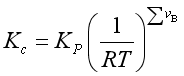 (19)
(19)
![]() 也只与温度有关,其单位是
也只与温度有关,其单位是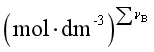
![]() 是以摩尔分数表示的平衡常数,定义
是以摩尔分数表示的平衡常数,定义
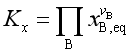 (20)
(20)
因 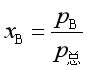
所以 ![]() (21)
(21)
与其他平衡常数不同,![]() 与温度和总压
与温度和总压![]() 有关,是量纲一的量。
有关,是量纲一的量。
综合(17),(19) 及 (21)得
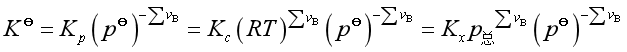
当![]() 时 ,
时 ,![]() =
=![]() =
=![]() =
=![]()
2.实际气体化学反应
实际气体B组分的化学势为
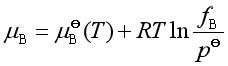
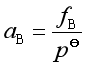
所以 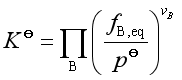 (22)
(22)
式(22)是实际气体化学反应标准平衡常数的表达式,由于![]() 只是温度的函数,故
只是温度的函数,故![]() 也只是温度的函数,与压力无关。
也只是温度的函数,与压力无关。
实际气体反应中也有经验平衡常数![]()
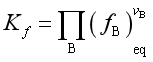 (23)
(23)
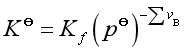 (24)
(24)
![]() 也只与温度有关,它的单位与压力相关。
也只与温度有关,它的单位与压力相关。
二、液相反应的平衡常数
1.液态混合物
若参与反应的各组分形成理想液态混合物,则![]()
![]()
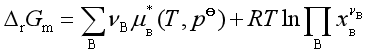
平衡时,![]()
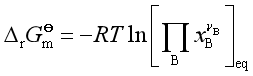
所以标准平衡常数 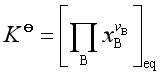 (25)
(25)
若参与反应的各组分组成实际液态混合物,则以活度代替物质的量分数,即
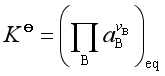 (26)
(26)
液态混合物反应的![]() 也只是温度的函数,是量纲一的量。
也只是温度的函数,是量纲一的量。
此系统的经验平衡常数是![]() ,其表达式与式(26)一致,故也是量纲一的量。严格说来,由于活度与温度、压力、浓度有关,故
,其表达式与式(26)一致,故也是量纲一的量。严格说来,由于活度与温度、压力、浓度有关,故![]() 应与压力有关。但由于压力对活度影响较小,在压力变化不大时,可视为
应与压力有关。但由于压力对活度影响较小,在压力变化不大时,可视为![]() 只与温度有关。
只与温度有关。
2.溶液反应
若参与反应的物质均溶于同一种溶剂,并且均与溶剂构成理想稀溶液,溶剂本身不参与反应,例如在CHCl3溶液中,N2O4离解成NO2即属于这种情况。
因为 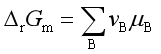
若物质的浓度用物质的量浓度表示
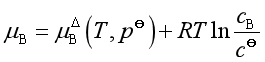
平衡时 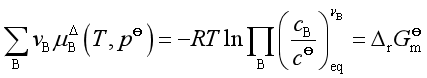
即 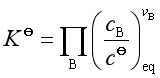 (27)
(27)
![]() 就是这种稀溶液反应的标准平衡常数,它仅是温度的函数,是量纲一的量。
就是这种稀溶液反应的标准平衡常数,它仅是温度的函数,是量纲一的量。
这种情况下反应的经验平衡常数是![]() 以下式表示:
以下式表示:
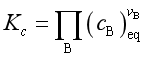 (28)
(28)
可见,![]() 与
与![]() 量值上相等,但
量值上相等,但![]() 的单位为
的单位为![]() 。
。
若溶剂溶质均参加反应,且彼此构成实际溶液,此时
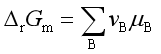
溶剂和溶质的化学势分别为
溶剂: ![]()
溶质: ![]()
从而可得 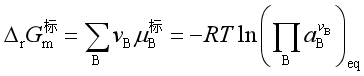
根据 ![]()
可得 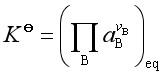
![]() 即为此种反应系统的标准平衡常数,习惯上我们称它为“杂平衡常数”,这是由于
即为此种反应系统的标准平衡常数,习惯上我们称它为“杂平衡常数”,这是由于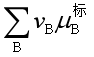 中,溶剂和溶质的标准态是完全不同的。
中,溶剂和溶质的标准态是完全不同的。
三、复相反应的平衡常数
若参与反应的物质处于不同的相态,化学反应就会在相与相的界面上发生,这种反应称为多相反应或“复相反应”。
设有复相反应
并设参与反应的物质共有N种,其中有n种是理想气体,(N-n)是纯凝聚相。又设气体压力都不大,可视为理想气体;所有的凝聚物都不构成溶液或固溶体,即各自都以纯态存在。此时反应的摩尔反应吉布斯自由能为
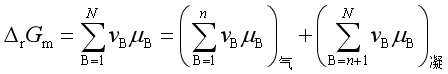
平衡时![]() =0。又因为理想气体的
=0。又因为理想气体的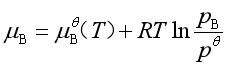 ,代入
,代入![]() 的表达式,即得平衡时
的表达式,即得平衡时
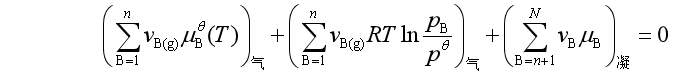
或
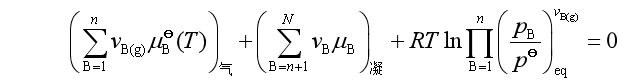 (29)
(29)
在式(29)中,第一项是各理想气体标准态的化学势之和,第二项是各凝聚相化学势之和。由于已假设凝聚物都以纯态存在,常压下纯凝聚态物质的化学势可近似等于其标准态化学势,故第二项又是凝聚物质标准态的化学势之和。若将一、二两项合并,可得参加反应的所有物质的标准态化学势之和,写为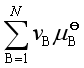 ,并有
,并有
 (30)
(30)
因此式(29)可写作
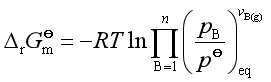 (31)
(31)
则标准平衡常数
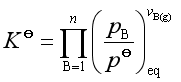 (32)
(32)
式中![]() 是参加反应的各理想气体组分的分压,
是参加反应的各理想气体组分的分压,![]() 是各理想气体组分的化学计量数。可见,复相反应的标准平衡常数只与参加反应的理想气体组分有关,与凝聚相组分无关。显然,复相反应的
是各理想气体组分的化学计量数。可见,复相反应的标准平衡常数只与参加反应的理想气体组分有关,与凝聚相组分无关。显然,复相反应的![]() 也只是温度的函数,一定温度下,
也只是温度的函数,一定温度下,![]() 有定值。例如,对于反应
有定值。例如,对于反应
CaCO3(s) = CaO(s) + CO2(g)
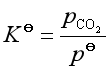
经验平衡常数 ![]() (33)
(33)
故等温下,CO2的平衡分压是个定值,与CaCO3,CaO的量无关。所以,人们将一定温度下凝聚物质分解达平衡时的压力称为该物质的分解压。CaCO3的分解压就是平衡时CO2的分压。在室温下, CaCO3的分解压很小,实际上并不分解。随着温度升高,分解压增大,当![]() 时的温度,称为CaCO3的分解温度。CaCO3的分解温度约为897℃,此时由于
时的温度,称为CaCO3的分解温度。CaCO3的分解温度约为897℃,此时由于![]() 为100kPa,所以CaCO3(s)剧烈分解,像“沸腾”一样。
为100kPa,所以CaCO3(s)剧烈分解,像“沸腾”一样。
如果一种固体分解出两种气体,如
NH4Cl(s) = NH3(g) + HCl(g)
则 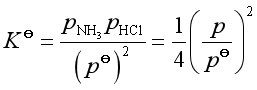
式中p为固体NH4Cl分解达平衡时系统的总压,即分解压。等温下,![]() 是定值,故p也是定值。
是定值,故p也是定值。
