一、简单级数反应

人们通常将反应级数为零和简单正整数的反应称为具有简单级数的反应，例如零级反应，一、二、三级反应等。应注意，具有简单级数的反应不一定是基元反应。本节讨论简单级数反应的速率方程及其特点。

1．零级反应

反应速率与物质浓度无关的反应，称为零级反应。

零级反应大多数是异相反应，最多的是在表面上发生的复相反应，例如

氧化亚氮在铂丝上的分解反应   2N₂O → 2N₂ + O₂       

高压下氨在钨丝上的分解反应   2NH₃ → N₂ +3H₂       

这些反应的速率之所以与物质浓度无关，主要是因为它们只有在金属催化剂的表面才能发生，若金属表面已被气体分子所饱和，则再增加气相浓度也不能改变表面上反应物的浓度，故反应速率不再依赖于气相浓度。另外，一些光化反应、表面电解反应等也为零级反应。

设零级反应的计量方程为 Ａ→Ｐ  若用反应物浓度（c）消耗来表示反应速率，则有

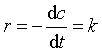
这是零级反应速率方程的微分式。将该式移项并积分            

得零级反应的速率方程的积分式为   

                              （13a)

或写作

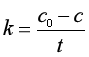                              （13b)

由此可见，零级反应的特点是：

（1）以反应物浓度c对时间t作图得一直线，直线斜率为 -k 。

（2）k的单位是[浓度]·[时间]^-1，如 mol·dm^-3·s^-1。

（3）如果将反应物浓度消耗一半所需的时间t_1/2称为半衰期，则当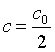时，得其半衰期为 ，可见零级反应的半衰期与起始浓度成正比。

以上三个特点可以作为判断零级反应的依据。

2．一级反应

反应速率与反应物浓度一次方成正比的反应，称一级反应。

多数复杂结构分子的热分解反应，分子内部重排列反应以及放射性元素的蜕变反应，都是一级反应。

若某一级反应A → P ，反应物浓度为c，则其速率方程的微分式可表示为

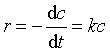                        (14)

移项，在 t = 0 到任意时刻t之间积分

   

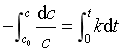
可得                     (15)

则一级反应速率系数为 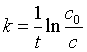                (16)

写成指数形式为              (17)

以上三式均为式（14）的积分式，即一级反应的动力学方程式。

有时为了计算上的需要，对A → P的一级反应，也可以用 a表示反应物A的起始浓度，用x表示t时刻产物的浓度，则t时刻反应物浓度为a－x；这时，一级反应的速率系数为

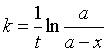             (18)

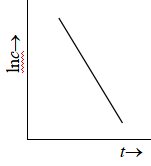
图2 一级反应的lnc～t图

根据上述化学反应动力学方程式，概括一级反应的特点有：

(1) 以lnc 对t 作图应得一直线，如图2，其斜率等于速率系数的负值(-k)。

(2) 由实验测定反应物在任意时刻t的浓度c，代入式(16)，即可得反应速率系数k，如对若干组t～c值求得若干k 值，k值应为一常数。一级反应速率系数k的单位为（时间）^-1，时间可用秒（s）、分（min）、小时（h）、天（d）、年（y）等来表示。

(3) 根据式(16)，当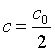时，得其半衰期为

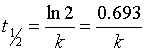                           (19)

由此可见，一级反应的半衰期与反应物浓度无关，而由速率系数决定。当温度一定时，一级反应的半衰期是个常数，这个特征常数可以作为判别一级反应的依据。

例1  某药物分解为一级反应，当它分解30% 即告失效。已知该药物样品的初浓度为5.0×10-3 kg·dm^-3 ，在室温25℃下放置20个月后浓度降为4.2×10^-3 kg·dm^-3 ，求该药物的半衰期及使用有效期为多少？

解  根据一级反应速率系数表达式并代入已知数据

  

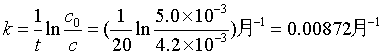
半衰期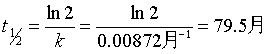   

有效期为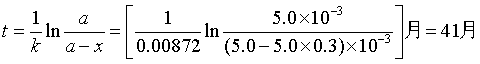   

3. 二级反应

反应速率与物质浓度二次方成正比的反应为二级反应。二级反应最为常见，碘化氢、甲醛的热分解反应，乙烯、丙烯、异丁烯的二聚反应，水溶液中乙酸乙酯的皂化反应等都是典型的二级反应。二级反应可能有二种类型 

(1)  A + B → P         r = k c_Ac_B  

(2)  2A → P            r = k C_A²

事实上，对反应（1），当反应物A、B为同一种物质时，即成为反应（2），可见反应（2）为反应（1）的特例。对于反应（1），若用a、b分别表示反应物A、B的初始浓度，用产物的浓度（x）变化来表示反应速率
A + B  → P

反应在t ＝0时浓度       a   b     0

反应t时刻浓度        a-x b-x   x

速率方程为 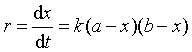               (20)

可分两种情况进行讨论：

设A和B的起始浓度相同，即a = b，则上式化为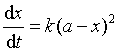 

移项，在t ＝ 0 至t之间积分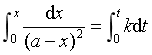                     

整理得 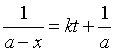            (21)

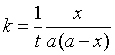      (22)

根据以上所述，二级反应的特点有：

(1) 从式（21）看出，以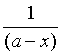对t作图应为一直线，直线斜率等于速率系数k。

（2）用实验测定任意时刻产物的浓度（x），代入式（22），即可求得速率系数k。同一温度下若干组实验得到的k值应该为一常数。二级反应速率系数k的单位是（浓度）^-1·（时间）^-1，通常以mol^-1·dm³·s^-1 表示。

(3) 当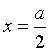 时，代入式（22），可求得半衰期为

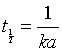                        (23)

上式表示起始浓度相同的二级反应的半衰期与起始浓度成反比关系，这可以作为判断二级反应的依据。

当二级反应的反应物Ａ与Ｂ的起始浓度不同，即a≠b时，将式 (20)移项并在t=0 至t 之间积分

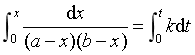
得 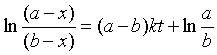        (24)

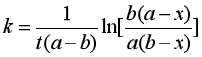整理得         (25)

式(24)表明这类二级反应 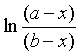与t成直线关系，直线斜率为 (a-b)k。由于a≠b ，所以半衰期只能分别对Ａ和Ｂ而言，而且数值上是各不相同的。

另外，对 A + B → P 的二级反应，当某一反应物数量保持大量时（浓度一般大20倍以上），可认为其浓度保持不变，因而使反应降为一级反应，例如蔗糖水解反应就是个典型例子，由实验可知，蔗糖水解为二级反应，其反应速率r = k ，当H₂O为大量时，r = k ´C_蔗糖，符合一级反应规律，这类反应称“准一级反应”。准一级反应的速率系数k´ 与二级反应的速率系数k具有不同的单位，准一级反应具有一级反应的特点。

对于第二种类型的二级反应   2A  →  P

速率方程为             

积分上式即可求得反应速率系数k。但应注意，k为与反应进度表示的反应速率r相对应的反应速率系数，该情况下，k与k_A不同，二者的关系是。

 

例2  NaDH+ 酶→酶-NaDH是二级反应，k = 1.2×107mol^-1·dm³·s-1  若NaDH与酶的起始浓度均为100μmol·dm^-3 时，求该反应的半衰期。

解  两反应物起始浓度相等的二级反应，半衰期与起始浓度成反比，故反应半衰期为

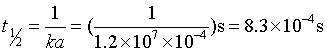
上述计算表明，对于气相反应，可以直接用压力代替浓度来计算速率系数k_p，它与用浓度计算的速率系数 k_c在数值及单位上均不相同。可以通过理想气体状态方程式进行换算。

4．n级反应

除了以上讨论的零级反应、一级反应、二级反应外，还有分数级反应乃至n级反应。为了总结化学反应速率方程式的规律，现通过对n级反应的分析来归纳说明。

对单一反应物A为n级（n≠1）的反应，若计量方程为 A→P ；用c表示反应物A的浓度，速率方程可写为

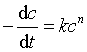                             （26）

移项，作不定积分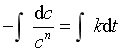                                    

得 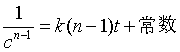        （27）

若设反应物的起始浓度为a，产物浓度为x，上式变为

          (28)

可见，若以 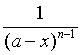  对t 作图，应为一直线，直线斜率等于k与（n-1）之乘积。这是求反应应速率系数的一种方法——作图法。

若将式（26）移项，作从时间t=0到任意时刻t 之间的定积分

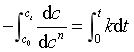
得 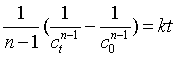          （29）

同样，上式也可写为 

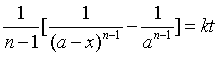              (30)

通过实验，求同一温度下不同时刻t时的产物浓度x，代入式（7.30），可求多个速率常数k值，这些k值应为一常数。这是求反应应速率系数的另一种方法。

当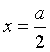时，，代入式（7.30），可求得n级反应的半衰期为

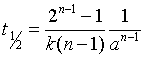                 (31)

式（31）也可化简为      

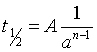                    (32)

其中，A为与反应级数相关的系数。

通过以上动力学分析，可知研究反应速率方程时，一般是先由微分方程导出积分式，再分析该速率方程的特征，如具有何种变量间的线性关系、半衰期与初浓度的关系等，之后才能进行相关物理量的计算。

表1列出具有简单级数反应的速率方程式及特征。人们常利用这些特征来判别反应级数及处理动力学问题。

 

注：a、b、c均为反应物起始浓度，x为产物浓度。

二、反应级数的确定

反应级数是重要的动力学参数之一，它显示了浓度对反应速率的影响，也能帮助我们探讨反应机理、了解真实反应过程，为化学反应器设计提供必不可少的数据。以下介绍确定反应级数的几种方法。

1．积分法（或尝试法）

根据各类速率方程的积分式确定反应级数的方法，称为积分法。通常由实验测定不同时刻t的反应物的浓度c数据，分别利用各级反应的c~t关系（式13a，15，21等）作图，若得直线，即为该关系所对应的反应级数。也可将c~t数据代入各级反应的速率系数表达式（式13b、16、22等），若计算结果得一常数，即为该式所对应的反应级数。无论作图或计算，都是利用速率方程的积分式进行尝试，所以又称尝试法。

积分法是一种常用的确定级数的方法，但是对那些实验时间持续不够长，转化率低的反应，此法显得不够灵敏，很难区分出具体的级数。

2．微分法

利用反应速率方程的微分式来确定反应级数的方法称为微分法。具体可以分为以下三种方法：

（1）图解微分法：

先讨论简单的反应 Ａ→Ｐ，设t时刻A的浓度为c，反应速率方程为

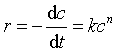
取对数得       ln r = lnk + n lnc      (33)

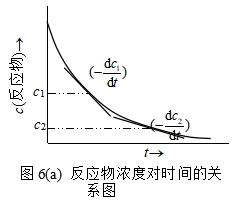
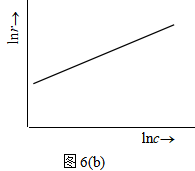
根据实验数椐作c～t图，在不同时刻浓度c₁  ，c₂ ，…各点上，求曲线的负斜率值 （）,即r₁ 、r₂…，如图6a所示。再用lnr对lnc  作图，若所设的速率方程是对的，则应得一直线，该线的斜率即为反应级数n，如图6b所示。

也可在一系列的r及c值中，任取2组数据（如r₁ 、c₁ 和r₂、c₂），代入（33）式并相减，求得反应级数n 

  

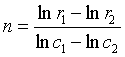
以上是通过反应系统在不同时刻的浓度变化而求得的级数，也称为时间级数。

      

(2)起始速率法：

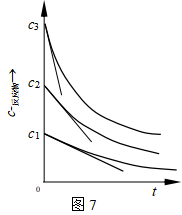
用微分法确定级数，还可以使用起始速率（r₀）法，即用不同的反应物起始浓度（c₀）做系列实验，作出几条c～t曲线（如图7），求各不同起始浓度曲线在t=0时的切线负斜率值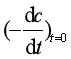，即不同r₀值。然后根据式(33)，以lnr₀ 对lnc₀作图，后继处理方法与图解微分法相同，直线斜率即反应级数n 。                                              

由于反应刚开始时的反应系统不受其它因素如产物、副产物等的干扰，因此求得级数较为可靠。所得级数是在                            
不同起始浓度下求得的，故也称为浓度级数。

                                      

（3）孤立法

当速率方程中含有多种物质，或反应速率方程有如下形式：，可以用孤立法求级数，所谓孤立法 是除某一反应物（如A）外，设法让其余反应物（如B、C）都大大过量，使它们的浓度在整个反应中近似不变，这样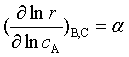，速率方程变为，即

ln r =αlnc_A + ln k′

利用作图等方法，可以求得Ａ的分级数α，再用同样方法求得Ｂ和Ｃ的分级数β和γ。

另外，有一种方法与孤立法类似，称为改变物质数量比例法：

设速率方程式为  ，若设法保持Ａ和Ｃ的浓度不变，而将Ｂ的浓度加大一倍，若反应速率也比原来加大一倍，则可以确定c_B 的指数b＝1。同理，若保持Ｂ和Ｃ的浓度不变而将Ａ的浓度加大一倍，若速率增加为原来的4 倍，则可确定c_A的指数a＝2。这种方法可应用于较复杂的反应。例如：

对气相反应，在某温度下：3 H₂ + N₂ → 2 NH₃  有下列速率数据。

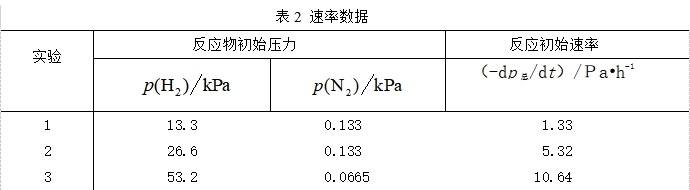
假设其速率方程形式为    
比较上述实验1和2可知，当不变而是原来的2 倍时，速率是原来的4倍，意味着x = 2 ；比较实验2和3，当是原来的2倍时，预期速率应是原来的4倍，但实际速率只是原来的2 倍，是预期倍数4的，原因是是原来的，这意味着 y = 1 ，可推知速率方程为

 

3.半衰期法

利用半衰期与起始浓度的函数关系求反应级数的方法称半衰期法。若反应物的起始浓度都相同（为a），从半衰期与浓度的关系（一级反应除外）式（32）可知

                                   

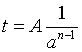
式中，反应级数 n≠1，A为比例系数。

(1)作图法：将上式改写为    

ln t.1/2 =(1－n) ln a+ ln A  （34）

实验求出不同起始浓度a 及其对应半衰期t_1/2 的若干组数据，以ln t_.1/2 对lna作图，从斜率便可求得反应级数n。

(2)计算法：如果只用两组不同起始浓度a和a'作实验，求得t_1/2 和t'_1/2值，则将实验数值代入（32）式并相除，得

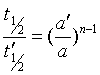
两边取对数并整理得

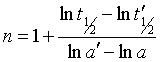             　　　　（35）

若已知反应完成1/3、1/4等的寿期t_1/3 、t_1/4 ，也可以用类似上述半衰期法求算反应级数。

例5  起始浓度相同的 1，2－二氯丙醇与 NaOH 在298Ｋ时发生环化反应，反应式为

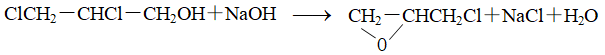
实验数据见下表，试求该反应的级数。

解 根据实验数据，可用半衰期法（计算法）来求反应级数，将数据代入（35）式，得

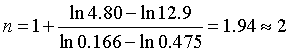
即此反应为二级反应。