第六章 化学动力学基础
 知识点五:温度对反应速率的影响
知识点五:温度对反应速率的影响
温度对化学反应速率的影响是早已被人们了解的事实,多数情况下,温度升高, 反应速率增大。但对于不同类型的反应,温度对反应速率的影响是不相同的,大致有图12表示的五种类型:

图12 反应速率和温度关系的几种类型
第Ⅰ种类型是反应速率随温度升高而逐渐加快。它们之间为指数关系,这种类型最常见,称阿仑尼乌斯型。第Ⅱ种是有爆炸极限的反应,其特点是温度升高到一定程度后,反应速率迅速增大。第Ⅲ种是酶催化反应及受吸附控制的多相催化反应,反应速率有极大值 。第Ⅳ种是某些烃类气相氧化、煤的氧化等反应,反应速率既有极大值,又有极小值。第Ⅴ种是反应速率随温度升高反而下降的反常类型,如反应2NO+O2 →2NO2。本节仅讨论常见的第I种类型。
一、范特霍夫规则
1884年,范特霍夫根据实验归纳得到一近似规则;温度每升高10K, 反应速率大约增加2 ~ 4 倍。若以kT 和kT+10K分别表示在T和T+10K时的速率系数,范特霍夫规则表示为:
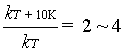 (50)
(50)
根据此式可粗略估计温度对反应速率的影响。
二、阿仑尼乌斯方程式
1889年阿仑尼乌斯(Arrhenius)通过大量实验与理论的论证揭示了反应速率对温度的依赖关系,提出了阿仑尼乌斯经验公式。公式可用三种不同的数学式表示:
指数式 ![]() (51)
(51)
对数式 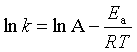 (52)
(52)
微分式 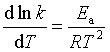 (53)
(53)
式中A称为指(数)前参量,A与k有着相同的量纲。对于不同的反应其数值也不同;Ea称为反应的活化能,有时也称阿仑尼乌斯活化能;因为它是通过实验数据求得,也称实验活化能。若温度变化范围不大Ea可视为常数,将式(53)作定积分可得
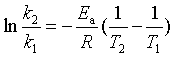 (54)
(54)
式(54)为阿仑尼乌斯公式的定积分式,式中 k1 、k2 分别为温度 T1 、T2 下的速率系数。
阿仑尼乌斯方程式最初是从气相反应中总结出来的,后来证明对液相中的反应也同样适用。利用以上公式,人们可以进行有关反应活化能Ea、指前参量A、不同温度下的的速率系数等的计算,其中活化能Ea和指前参量A是动力学研究中的重要参量。
例6 对乙醛分解的二级反应,测得如下数据,试求Ea值

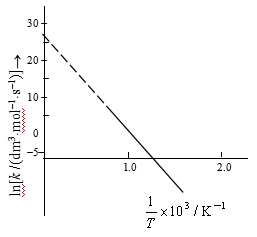
解 根据以上数据计算出对应lnk值及1/T值,并以lnk对1/T作图得一直线(图13),由图求得直线斜率为-2.207×104K,因此
Ea= -[8.314×10-3×(-2.207×104) ] kJ·mol-1=183.5kJ·mol-1
![]()
例7 丙酮(撑)二羧酸CO(CH2COOH)2在水溶液中分解,已知283K时,k(283K) = 1.08×10-4s-1,333K时k(333K) = 5.48×10-2s-1, 求反应在303K时的速率系数k303K值。
解 利用阿仑尼乌斯方程的定积分式
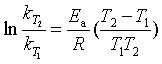
代入有关数椐得
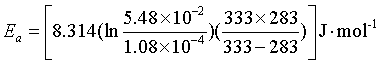
= 97.6 kJ·mol-1
由式(54)可得
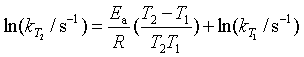
若此时将T2视为303K,则
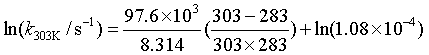
k303K=1.67×10-3s-1
此值与实验值1.63×10–3 s-1很符合。
一定温度下,反应应速率系数k决定于指前参量A及活化能Ea。在这二个重要的动力学参数中,起主要作用的是Ea,因为活化能Ea处在公式中的指数项位置,它对反应速率系数k的影响较大。一定温度下,活化能越小的反应k值越大。活化能如有较小的差别,将会给k值带来很大的差异。若有两个反应,在常温下发生,它们的A值相等,当Ea相差2kJ·mol-1时,它们的反应速率相差2倍;当Ea相差4 kJ·mol-1时,速率相差约5倍;当Ea相差6 kJ·mol-1时,速率相差约12倍了。一般化学反应的活化能约在40~400 kJ·mol-1之间。
在阿仑尼乌斯经验式中,活化能Ea被视为是与温度无关的常数,这在一定的温度范围内与实验结果相符,但是对于温度范围较宽或者是较复杂的反应,lnk对1/T作图就不是一条很好的直线,这说明了活化能Ea与温度有关,而且阿仑尼乌斯经验式对某些复杂的反应可能不适用。在较宽温度范围内,有人提出了修正的三参量方程公式
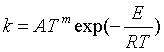
或 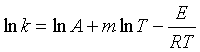 (55)
(55)
式中的A、E、m均由实验确定,将式(55)对T微分,代入式(53),得
Ea= E + mRT (56)
上式表明了阿仑尼乌斯活化能与温度的定量关系。一般的实验值m较小,在温度不太高时,阿仑尼乌斯经验式仍与实验结果较好相符。
三、活化能及估算
1.活化能
阿累尼乌斯认为在任何化学反应中,不是所有分子间的碰撞都能发生反应,只有少数具有一定能量的分子间的碰撞才能发生反应。 将这种能发生反应的分子称为活化分子,将一摩尔普通分子转变为活化分子所需要的摩尔能量称为活化能。
阿累尼乌斯提出了活化能的概念,但对活化能的解释不够明确,特别是把活化能看作与温度无关的常数,这与许多实验事实不符。随着科学的发展,1925年,托尔曼(Tolman)用统计热力学方法推导出
Ea=〈E*〉-〈E〉
式中〈E*〉为活化分子(即发生反应的分子)的平均摩尔能量,〈E〉为反应物分子的平均摩尔能量,活化能是活化分子的平均能量与反应物分子的平均能量之差。由于〈E*〉和〈E〉都与温度有关,Ea应是温度的函数,但有些情况下二者的温度效应可能彼此抵消,此时Ea则与温度无关。
2.正、逆反应活化能
将活化能看成是分子实现反应时需要克服的能垒,这种能垒对正、逆反应都存在。因为根据微观可逆性原理(principle of microreversibility),一基元反应的逆反应必然也是基元反应;正反应和逆反应必通过相同的过渡态。
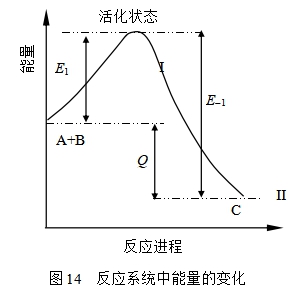
根据这一原理,用图7.14表示反应系统中能量变化关系:状态I表示反应物 A+B的平均能量,状态II表示产物分子C 的平均能量,反应物分子必须具备较平均能量高出E1的能量才能达到活化状态,越过能垒而变成产物分子,E1为正反应的活化能,同理,E-1为逆反应的活化能。因为一定温度下,系统从能量低的状态到高的状态要吸热,从能量高的状态到低的状态要放热, 从图中看出,当反应物A+B从I的状态达到活化状态吸收的能量为E1,再从活化状态到产物C的Ⅱ状态,放出能量E-1,反应的热效应为
E1 — E–1 = Q ( 57)
当E1>E-1时,为吸热反应, 当E1 < E–1时,为放热反应。这一结论也可以利用阿仑尼乌斯公式和化学反应等压方程来建立:设在温度T时存在一等压的对峙反应,正、逆反应的速率系数分别为k1和k–1 ;活化能分别为E1和E-1 ,则根据 阿仑尼乌斯公式,有 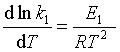 和
和 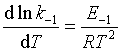 ,两式相减得
,两式相减得
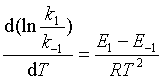
因为 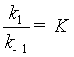 ,即平衡常数,代入上式为
,即平衡常数,代入上式为
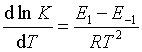 (58)
(58)
等压方程为
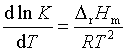 (59)
(59)
将式(58)与式(59)相比较,可得出E1-E-1 =ΔrHm,ΔrHm为反应的摩尔焓变,恒压时ΔrHm=Qp,其量值等于摩尔恒压反应热。若设在温度T时存在一等容的对峙反应,则同理可得出E1-E-1=ΔrUm,此时,QV=ΔrUm。可见对基元反应而言,正、逆反应活化能之差为反应热效应(等压热效应或等容热效应),即式(57)。
3.表观活化能
从实验中通过测定不同温度下的速率系数求得的活化能Ea,只对基元反应(或简单反应)才有明确的意义,而对于非基元反应,活化能实际上是组成该反应的各基元反应活化能的特定组合,称为表观活化能。以下分析表观活化能Ea和各基元反应活化能Ei之间的关系:
例如碘化氢的合成反应 H2+I2![]() 2HI 由三个基元反应组成。其中,有二个是快速反应,相互关联,并很快达平衡;另一个为速率控制步骤的慢反应,故将反应历程表示为
2HI 由三个基元反应组成。其中,有二个是快速反应,相互关联,并很快达平衡;另一个为速率控制步骤的慢反应,故将反应历程表示为
(1) ![]()
(2) ![]()
从基元反应(1)(2)得
![]()
![]()
![]()
HI的生成速率为
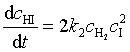 (60)
(60)
由基元反应(1)得
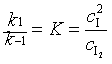
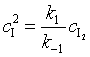
代入式(60)后得到反应速率表达式
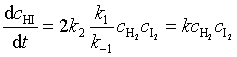 (61)
(61)
可见
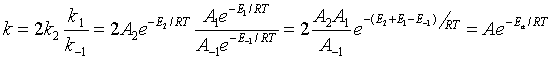
式中对比得
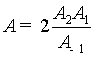 ; Ea= E2 + E1- E-1
; Ea= E2 + E1- E-1
即表观活化能Ea等于各基元反应活化能的代数和。如果知道各基元反应活化能。 就能计算出反应的表观活化能, 上例中E1=151kJ·mol-1, E2 =21 kJ·mol-1, E-1 ≈0, 所以Ea=(21+151-0)kJ·mol-1≈172 kJ·mol-1。
4.从键能估算活化能
基元反应的活化能,一般可以从反应所涉及到的化学键的键能来估算。虽然是粗略的,但对分析反应速率仍有帮助。
(1)分子裂解为自由基的基元反应,例如 Cl-Cl + M →2Cl·+ M
Cl·表示氯分子裂解后的氯自由基,在基元反应中,需要断裂的仅是Cl-Cl键,且无新键生成。故反应所需要的活化能即为断裂化学键所需要的键能 Ea = εCl-Cl
(2)自由基与分子间的基元反应
例如 Cl· + H2 → HCl + H·
H· + Cl2 → HCl + Cl·
这类反应的通式可以写为 A· + B-C → A-B + C· ,由于反应中有一活性很大的自由基参加,当正反应为放热反应时,所需活化能约为需改组化学键能的5.5%,即Ea= 0.05εB-C。
注意,该规则只适用于放热反应。若当正反应为吸热反应时,由图(14)可知,其活化能等于逆反应活化能与反应热之和,故此时,Ea =0.05εA-B +∣Q∣
(3)自由基之间复合的基元反应
例如 Cl· + Cl· + M → Cl2 + M
自由基的活性很大,复合时不需断裂任何键,只要在反应过程中存在接受耗散能量的第三体M,反应就能进行,故反应活化能一般为零, Ea =0。
(4)分子之间的基元反应,
这类反应通式可写为 A-B + C-D → A-C + B-D ,在反应中,需要断裂的是A-B键和C-D键,在反应过程中,被活化的分子先形成活化络合物,再转化为产物,在活化络合物 中,需断裂的键已被削弱,要形成的新键基本构成,所需的活化能必小于被断裂键能的总和,约占被断裂键能总和的30%,即Ea= 0.30 (εA-B +εC-D) 。
