第六章 化学动力学基础
 知识点八:反应速率理论
知识点八:反应速率理论
在反应速率理论的发展过程中,为了探讨化学反应速率的内在规律,在阿仑尼乌斯公式的基础上,借助于分子运动论和分子结构的知识,先后形成了碰撞理论、过渡状态理论、单分子反应理论等动力学研究中的基本理论。
一、碰撞理论
碰撞理论(collision theory)是根据分子运动理论提出来的,它认为两个分子要发生反应,首先必须碰撞,但有的碰撞并不发生反应,只有那些能量比普通分子高的活化分子才能发生有效的碰撞引起反应。若将分子在单位时间、单位体积内的碰撞次数称为“碰撞频率” (Z),将能发生反应的有效碰撞在总碰撞中占的分数称为“反应碰撞分数”或“有效碰撞分数”(q)。碰撞理论认为,可以用单位时间、单位体积内的有效碰撞次数来代替反应速率,所以其速率(r)可用下式计算
反应速率(r)=碰撞频率(Z)![]() 反应碰撞分数(q)
反应碰撞分数(q)
例如,对于A+B![]() P的反应,简单的碰撞理论认为其速率为
P的反应,简单的碰撞理论认为其速率为
r = ZAB ![]() q
q
式中ZAB及q可以分别单独计算。
在简单的碰撞理论中,采用了刚性模型。设 A、B 两种分子都是完全弹性的、无压缩性的刚球,半径分别为rA和rB,运动速率各为![]() 和
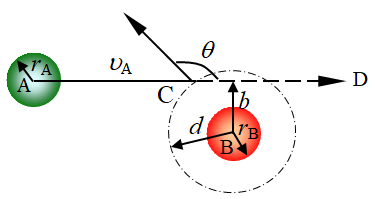
和![]() 。两个分子的碰撞过程实质是在分子力的作用下,先是分别接近,近到一定距离时,它们之间作用便以斥力为主,且斥力随分子间距减少而剧增,然后分子就改变了原来方向而远离,即完成一次碰撞。可见每次碰撞不一定有实质的分子接触。为使问题简化,设B静止不动,A以平均速度
。两个分子的碰撞过程实质是在分子力的作用下,先是分别接近,近到一定距离时,它们之间作用便以斥力为主,且斥力随分子间距减少而剧增,然后分子就改变了原来方向而远离,即完成一次碰撞。可见每次碰撞不一定有实质的分子接触。为使问题简化,设B静止不动,A以平均速度![]() 运动,碰撞时将两个分子靠近的最短距离b称为碰撞参数,b是从B的中心到趋近路径的延长线ACD的垂直距离,d为有效碰撞直径(
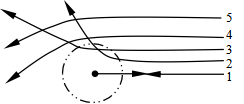
运动,碰撞时将两个分子靠近的最短距离b称为碰撞参数,b是从B的中心到趋近路径的延长线ACD的垂直距离,d为有效碰撞直径(![]() )。一旦发生碰撞,A就被偏转一个角度θ,其值取决于b(见图15)。分子碰撞运动方向发生改变示意图如16所示:路径1:b=0,θ=
)。一旦发生碰撞,A就被偏转一个角度θ,其值取决于b(见图15)。分子碰撞运动方向发生改变示意图如16所示:路径1:b=0,θ=![]() ,分子发生迎头碰撞;路径4、5:b>d,θ=0,分子不发生碰撞;路径2、3:0<b<d,0<θ<
,分子发生迎头碰撞;路径4、5:b>d,θ=0,分子不发生碰撞;路径2、3:0<b<d,0<θ<![]() ,分子发生碰撞。于是可以定义一个半径为(rA+rB)的圆作为碰撞的有效截面,称为碰撞截面,截面积σ为
,分子发生碰撞。于是可以定义一个半径为(rA+rB)的圆作为碰撞的有效截面,称为碰撞截面,截面积σ为
σ=![]() (rA + rB)2 =
(rA + rB)2 =![]() d2 (71)
d2 (71)
下面,将分别计算碰撞频率(ZAB)和反应碰撞分数(q)。
1.碰撞频率(![]() 和
和![]() )
)
设单位体积内有nB个静止不动的B分子,A分子以相对平均速率![]() 运动,将与 A 轨迹附近,碰撞有效截面积为
运动,将与 A 轨迹附近,碰撞有效截面积为![]() d2范围内的空间中的任一B分子发生碰撞。则在单位时间内A分子的碰撞体积为
d2范围内的空间中的任一B分子发生碰撞。则在单位时间内A分子的碰撞体积为![]() ,能碰撞到的 B 分子数即碰撞数为
,能碰撞到的 B 分子数即碰撞数为![]() 。若有nA个A分子穿越碰撞体积,则在单位时间内,A、B的碰撞总数即碰撞频率便为
。若有nA个A分子穿越碰撞体积,则在单位时间内,A、B的碰撞总数即碰撞频率便为
![]() (72)
(72)
在温度T 时,气体分子的运动速率服从麦克斯韦速率分布。
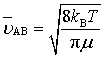
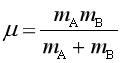 (73)
(73)
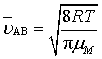
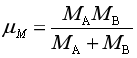 (74)
(74)
上面两式中, kB为玻尔兹曼常量,R为摩尔气体常量,μ为折合质量,m为每个分子的质量,M 为分子的摩尔质量。用式(74)代入式(72)得
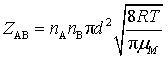 (75)
(75)
若A 、B的量改用物质的量浓度![]() 、
、![]() 时,
时,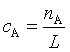 ,
,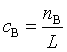 (L为阿佛加德罗常量),则
(L为阿佛加德罗常量),则![]() ,
,![]() ,代入式(75),得不同种分子碰撞频率
,代入式(75),得不同种分子碰撞频率![]() 为
为![]()
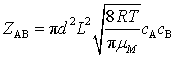 (76)
(76)
若系统中只有一种分子A,![]() ,
,![]() ,每次碰撞都需要两个A分子,为了避免重复计算,要将碰撞次数除以2,代入式(76)并整理得到同种分子的碰撞频率
,每次碰撞都需要两个A分子,为了避免重复计算,要将碰撞次数除以2,代入式(76)并整理得到同种分子的碰撞频率![]() 为
为
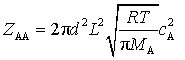 (77)
(77)
2.反应碰撞分数(q)
反应速率除与碰撞频率有关外,还与能量有关。只有那些沿分子间连心线AB方向的动能ε大于某临界值εC 的分子对才能实现有效碰撞从而发生反应。该临界值称为“阀能”或“临界能”,对于不同的反应,阀能εC 的值也不同,发生反应的必要条件是![]() 。根据麦克斯韦-玻尔兹曼分布定理,相对动能在ε+dε之间的分子所占的百分数为
。根据麦克斯韦-玻尔兹曼分布定理,相对动能在ε+dε之间的分子所占的百分数为
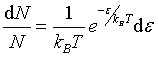
上式积分,可求得能量大于阀能(![]() )的活化分子所占的百分数,即反应碰撞分数
)的活化分子所占的百分数,即反应碰撞分数
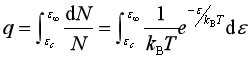
结果为 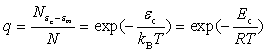 (78)
(78)
其中![]() ,
,![]() 相当于阿仑尼乌斯公式中的
相当于阿仑尼乌斯公式中的![]() ,但两者的物理意义是不同的。另外由理论模型可知,q的大小,不仅决定于碰撞时相对平动能的大小,还与碰撞的具体方式有关。
,但两者的物理意义是不同的。另外由理论模型可知,q的大小,不仅决定于碰撞时相对平动能的大小,还与碰撞的具体方式有关。
3. 用碰撞理论求算的速率系数(![]() )
)
对于 A+B![]() P 的反应,用简单碰撞理论分析可知其速率
P 的反应,用简单碰撞理论分析可知其速率
![]()
因为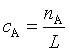 ,将式(76)、式(78),代入上式得
,将式(76)、式(78),代入上式得
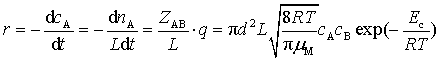 (79)
(79)
与二级反应速率公式 ![]() 比较,可知
比较,可知
不同分子反应的二级速率系数
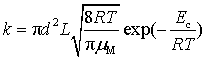 (80)
(80)
结合式(77),同理得到相同分子反应 2A![]() P 的二级速率系数为
P 的二级速率系数为
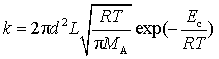 (81)
(81)
若将![]() 相当于
相当于![]() 时,与阿仑尼乌斯式
时,与阿仑尼乌斯式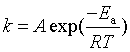 比较,结合式(80)、式(76),可看出指前参量A为
比较,结合式(80)、式(76),可看出指前参量A为
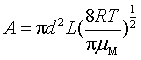 或
或 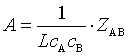 (82)
(82)
可见碰撞理论从微观上说明了基元反应速率与浓度幂乘积成正比的原因,并导出指前参量A是与碰撞频率![]() 有关的量。下面还可以对碰撞理论进行检验:
有关的量。下面还可以对碰撞理论进行检验:
(1)速率系数与温度的关系:按阿仑尼乌斯的微分式,活化能为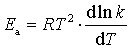 ,以碰撞理论导出的k表达式(81)代入上式,得
,以碰撞理论导出的k表达式(81)代入上式,得
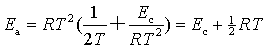 (83)
(83)
上式可见,阀能![]() 并不等于活化能
并不等于活化能![]() ,阀能与T无关,而活化能
,阀能与T无关,而活化能![]() 与T有关,常温下,
与T有关,常温下,![]() ,在温度变化范围不太大时,
,在温度变化范围不太大时,![]() 与
与![]() 相比可以忽略,
相比可以忽略,![]() >>
>> ![]() ,此时
,此时![]() ,所以
,所以![]() ,与阿仑尼乌斯式一致,这样,简单的碰撞理论预言的ln k 与
,与阿仑尼乌斯式一致,这样,简单的碰撞理论预言的ln k 与 ![]() 的直线关系与实验事实一致。但是当某一反应活化能很小,或温度较高,或温度变化范围较大,或实验要求较精确时,
的直线关系与实验事实一致。但是当某一反应活化能很小,或温度较高,或温度变化范围较大,或实验要求较精确时,![]() 项就不能忽略,此时
项就不能忽略,此时
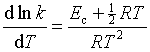 (84)
(84)
根据式(81),k可表示为 ![]() ,
,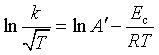 即 ,以
即 ,以 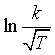 对
对![]() 作图才符合直线关系。这时用碰撞理论提出的指前参量与温度有关的式(82)来解释更符合实验结果。
作图才符合直线关系。这时用碰撞理论提出的指前参量与温度有关的式(82)来解释更符合实验结果。
(2)指前参量与方位因子: 利用碰撞理论并根据反应物的分子半径,分子的摩尔质量等有关数据及式(82),可计算出指前参量A计算,另外,若按阿仑尼乌斯式也可以从实验数据求得指前参量A实验,结果发现,多数反应的计算值大于实验值,见表3。 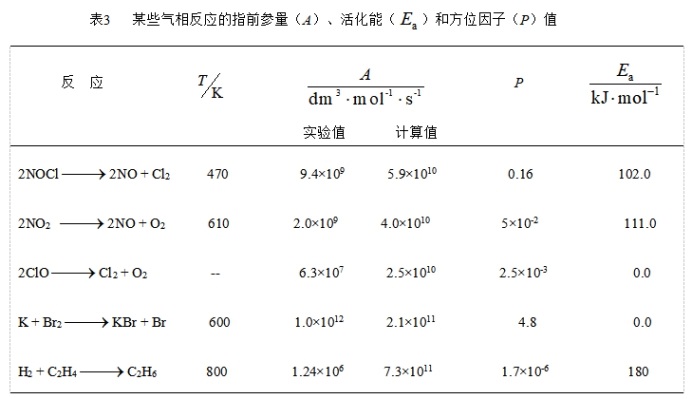
简单的碰撞理论是将反应物视为刚球模型,完全不考虑反应分子内部的结构、运动状态及相互作用,出现较大偏差是必然的。有人将偏差归因于方位效应。对多数反应,A计算大于A实验,推知其真实的碰撞截面要比![]() 小,所以提出用反应截面
小,所以提出用反应截面![]() 来代替
来代替![]() ,
,![]() 的大小与相对平动能有关,即也与碰撞方位取向有关(
的大小与相对平动能有关,即也与碰撞方位取向有关(![]() ),两者关系为
),两者关系为![]() ,其中P 称为方位因子(也称概率因子),P值也可从A的计算值与实验值求出,如表3 所示,即
,其中P 称为方位因子(也称概率因子),P值也可从A的计算值与实验值求出,如表3 所示,即
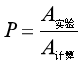 (85)
(85)
上述结果表明,并不是能量大于阀能的分子间碰撞都能引起反应,还要考虑一些其他的影响因素,如反应时分子之间的空间方位取向、电子飞跃等因素。例如:对 2HI![]() H2 + I2 的反应,有以下两种空间取向方式:
H2 + I2 的反应,有以下两种空间取向方式:
![]() ① (碰撞后,都能反应)
① (碰撞后,都能反应)
 ② (碰撞后,彼此弹开,不反应)
② (碰撞后,彼此弹开,不反应)
又如表7.3中显示 K + Br2 → KBr + Br 的反应,出现 A 的实验值大于计算值(P=4.8),这表明存在着某些特别有利于反应进行的因素,有人提出当 K 原子趋向 Br2 时,K 的价电子在碰撞参数 b>d 时,产生电子飞跃,飞向 Br2 ,形成的正、负离子间的库仑引力更有利于实现反应(电子飞跃机理,俗称“鱼叉模型”)。
引入方位因子(P)后,碰撞理论计算速率系数的公式(80)可写为:
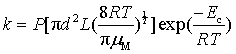 (86)
(86)
总之,k值的大小取决于:碰撞频率、能量分布、方位因子三个方面。目前可以对简单反应的P值做估计,而对复杂反应的P值,只能通过实验和计算值对比获得,如式(85),另外,对指前参量的物理意义认识也不明确,这是碰撞理论的局限。
例 12 计算反应 2 HI → H2 + I2 的速率系数,是应用碰撞理论最早的成功例子之一:此反应在556K时实验测定速率系数为k实验=1.75×10-7mol-1·dm3·s-1,活化能为184.13kJ·mol-1。根据HI粘度值得知它的分子直径为3.5×10-10m,试估算(1)反应的速率系数;(2)指前参量A 和方位因子P 的值。
解(1) 当阀能![]() 未知的情况下,令
未知的情况下,令![]() ,根据同种分子碰撞反应公式(7.81)
,根据同种分子碰撞反应公式(7.81)
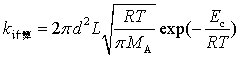
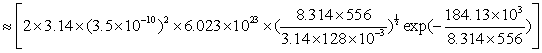 mol-1·m3·s-1
mol-1·m3·s-1
![]()
速率系数计算结果与实验值1.75×10-7mol-1·dm3·s-1比较符合。
解(2) 用式(83)的![]() 代入式(81)得
代入式(81)得
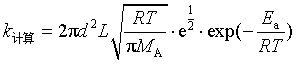
可知 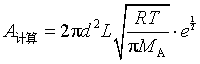
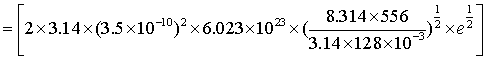 mol-1·m3·s-1
mol-1·m3·s-1
=8.19×107 mol-1·m3·s-1
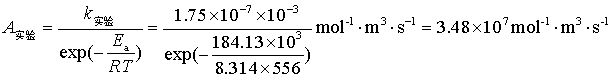
方位因子为 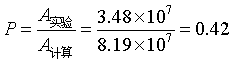
二、过渡态理论
1.基本假定
在统计力学和量子力学的发展过程中,化学动力学的过渡态理论也随之而建立。它既考虑了分子内部的结构,也考虑了粒子的运动状态。它的基本假设为:反应物到产物的反应过程中,反应物分子必须经过一定的过渡状态,但形成这种过渡态需要活化能,故把这种一定构型的过渡态又称为活化络合物。活化络合物与反应物分子之间建立化学平衡,总的反应速率是由活化络合物转化为产物的速率所决定。
例如反应 A+B—C ![]() [A···B···C]≠ → A—B+C
[A···B···C]≠ → A—B+C
当反应原子A沿B—C轴线逐渐接近B—C分子时,B—C中的化学键逐渐松弛和被削弱,原子A与B之间形成一种不稳定的新键,由于两个分子的电子云之间和原子核之间都有电斥力,当分子接近时,体系的势能随之增加,到了形成过渡状态活化络合物 [A···B···C] ≠ 时,体系的势能最大。 [A···B···C] ≠很不稳定,可能分解变为产物,也可能重新变回反应物,活化络合物分解为产物的速率等于反应速率。
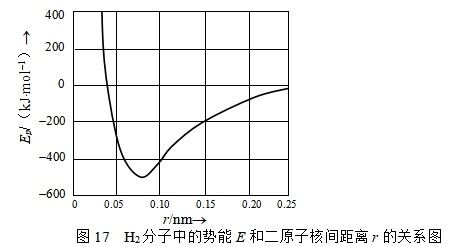
2.利用过渡态理论计算反应速率系数
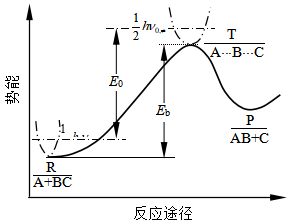
图20 势能面剖面图
过渡态理论认为,反应物在向生成物转化的过程中,获得能量越过能垒形成活化络合物,一旦形成活化络合物就会向生成物转化, 过渡态是自反应物向产物过渡的一个不折回点(对于过渡态可能分解回反应物的个别反应 的情况暂不作讨论)。过渡态活化络合物向产 物转化是整个反应的速控步骤,为了求得活化络合物的浓度(c≠),可以作一个假设,假设反应物与活化络合物之间存在一个快速达到的化学平衡,然后活化络合物再转化为产物。
设某气体反应为
A+B—C ![]() [A···B···C]≠
[A···B···C]≠ A—B + C
A—B + C
![]() 为生成活化络合物的压力平衡常数。已知
为生成活化络合物的压力平衡常数。已知
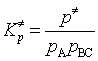 (88)
(88)
则活化络合物的压力
![]()
因活化络合物沿反应坐标方向的每一次振动都导致它的分解而形成产物,所以活化络合物的分解速率不仅与其压力(或浓度)有关,也与其不对称的伸缩振动频率![]() 有关,即反应速率应为
有关,即反应速率应为
![]() (89)
(89)
根据量子力学及能量均分定律可知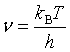 (h为普朗克常量),代入上式
(h为普朗克常量),代入上式
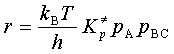 (90)
(90)
与二级动力学方程式![]() 对照,可知反应速率系数
对照,可知反应速率系数![]() 为
为
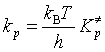 (91)
(91)
从上式可知,只要用热力学的方法求出![]() 的值,就可计算出
的值,就可计算出![]() 值。压力平衡常数
值。压力平衡常数![]() 需借助于标准平衡常数
需借助于标准平衡常数![]() 来表示
来表示
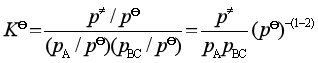
写成一般式为
![]()
即 ![]() (92)
(92)
若以![]() 、
、![]() 、
、![]() 分别表示活化络合物与反应物间的标准摩尔吉布斯自由能变(活化吉布斯自由能)、标准摩尔焓变(活化焓)、标准摩尔熵变(活化熵),根据热力学基本关系式可知
分别表示活化络合物与反应物间的标准摩尔吉布斯自由能变(活化吉布斯自由能)、标准摩尔焓变(活化焓)、标准摩尔熵变(活化熵),根据热力学基本关系式可知
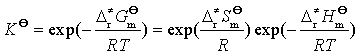 (93)
(93)
将式(92)、式(93)代入式(91)得
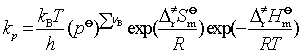 (94)
(94)
对于前面的双分子反应,该式可写为
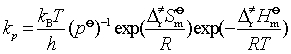 (95)
(95)
应注意的是,按照上式求得的是用压力表示的速率系数,对等容的双分子气相反应,![]() ,故可得上述反应的浓度速率系数为
,故可得上述反应的浓度速率系数为
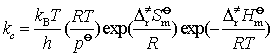 (96)
(96)
式(95)和式(96)为过渡态理论的热力学形式,它们能适用于任何形式的基元反应,原则上,只要知道活化络合物的结构,就可以从理论上推出![]() 和
和 ![]() ,从而计算出速率系数。以上两式还说明活化熵和活化焓共同影响着反应速率,但它们对 k 的影响作用是相反的:例如有的反应活化焓很大,使
,从而计算出速率系数。以上两式还说明活化熵和活化焓共同影响着反应速率,但它们对 k 的影响作用是相反的:例如有的反应活化焓很大,使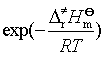 值很小,但若其活化熵很大,反应速率系数 k依然能很大。蛋白质的变性反应就是如此,虽然其
值很小,但若其活化熵很大,反应速率系数 k依然能很大。蛋白质的变性反应就是如此,虽然其![]() 高达420kJ·mol-1,但
高达420kJ·mol-1,但![]() 也大,故反应速率仍很大。
也大,故反应速率仍很大。
3 过渡态理论与阿仑尼乌斯公式的比较
过渡态理论热力学公式中的![]() 和
和![]() 与阿仑尼乌斯式中的活化能Ea和指前参量A的关系可以推导如下:
与阿仑尼乌斯式中的活化能Ea和指前参量A的关系可以推导如下:
将式(96)取对数并对温度微商可得
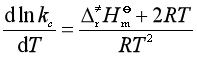 (100)
(100)
上式与阿仑尼乌斯定义式(53)对照可知,对等容的双分子气相反应,
![]() (101)
(101)
当反应分子数为 n时,因为![]() ,故式(796)变为
,故式(796)变为
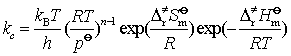 (102)
(102)
同理,将上式取对数并对温度微商可得
![]() (103)
(103)
温度不高时, ![]() (104)
(104)
若将式(96)与阿仑尼乌斯指数式(51)对比可知,对等容的双分子气相反应
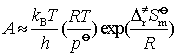 (105)
(105)
可见,指前参量A与形成过渡态时的熵变有关。
三、动力学中的各种活化能
活化能的建立,对化学反应的速率理论起了很大的作用。化学动力学中曾引入几个活化能:阿仑尼乌斯公式中的![]() ,碰撞理论中的
,碰撞理论中的![]() (阀能),过渡态理论中的
(阀能),过渡态理论中的![]() (能垒),另外还有统计热力学中计算络合平衡常数时涉及到的
(能垒),另外还有统计热力学中计算络合平衡常数时涉及到的![]() 。它们的物理意义各不相同,但在数值上有一定的关联。以上除
。它们的物理意义各不相同,但在数值上有一定的关联。以上除![]() 为唯象宏观量外,
为唯象宏观量外,![]() 和
和![]() 都是在反应速率理论发展过程中,由相应的模型提出的,它们只适用于各相关的速率理论。各活化能之间的关系已在前面相关内容中阐明,这里不再赘述。
都是在反应速率理论发展过程中,由相应的模型提出的,它们只适用于各相关的速率理论。各活化能之间的关系已在前面相关内容中阐明,这里不再赘述。
