一、 基本内容
化学动力学的基本任务是研究化学反应的速率和机理，以及各种因素对反应速率的影响，同时研究反应速率方程等化学动力学普遍规律。通过本章的学习，读者应掌握浓度、温度、催化剂因素对化学反应速率的影响规律；掌握如反应级数、速率系数、活化能、指前参量等反应系统的特性；了解研究化学动力学的理论方法，即从宏观层次上了解由基元反应构成的总反应过程的机理；以及从更深层次了解基元反应的速率理论。
（一）反应速率
设化学反应的计量方程为0＝
（
为物质B的化学计量数）
对于体积恒定的反应系统，反应速率定义为: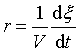 
式中V为体积，ξ为反应进度，t为时间。
由于dξ=
， 上式也可以写为: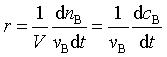 
设定容条件下，反应 aA+ bB 
dD + eE
则反应物消耗速率为: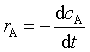
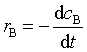
产物生成速率为: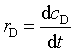
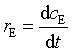
反应物消耗速率、产物生成速率与反应速率之间的关系为:
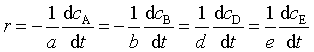
即:
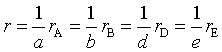
（二）基元反应的质量作用定律
对于基元反应 aA+ bB 
P
其质量作用定律表示为:
该式表示基元反应的速率与所有反应物浓度项的幂乘积成正比，其中浓度指数恰是反应式中各相应物质化学计量数的绝对值。其中，比例系数k为基元反应的速率系数。质量作用定律只适用于基元反应。
基元反应中反应物分子数的总和称为“反应分子数”。
(三）反应速率方程（反应动力学方程）
一定温度下，表示化学反应系统中反应速率与反应物的浓度间函数关系的方程式称为反应速率方程（有时也与产物浓度有关）。反应
aA+ bB 
dD + eE
若通过实验测定反应速率方程为:
则方程中α和β分别为A和B的级数，α+β＝n为反应的总级数；k为速率系数。
（四）半衰期与分数寿期
1.半衰期t1/2：反应物消耗掉一半所需要的时间。
2.分数寿期tb/a：反应物消耗掉某一分数b/a时所需要的时间。
不同级数的化学反应，半衰期与分数寿期有着不同的规律及其求算公式。
（五）具有简单级数反应的速率公式及其动力学特征
1.一级反应
反应速率与反应物浓度的一次方成正比的反应称为一级反应。例如 
。
对以及反映的速率方程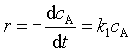
求定积分后，克的速率方程的积分式: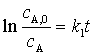
也可以产物浓度x表示，即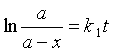 
（
为A的起始浓度）
一级反应的特点是：
（1）浓度与时间的线性关系为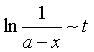 
；
（2）半衰期为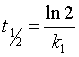 
，半衰期与反应物的初始浓度无关；
（3）反应速率系数k的量纲为 
。
2. 二级反应
反应速率与反应物浓度的二次方成正比的反应称为二级反应。例如 
；
。二级反应有以下两种情况：
（1）反应物A、B的初始浓度相同（a=b）
速率方程的微分式为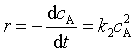 
速率方程的定积分式为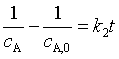 
若以产物浓度（χ）表示，则 
（
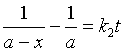为A的初始浓度）
此类二级反应的特点是
1）浓度与时间的线性关系为 ；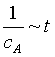
2）反应的半衰期为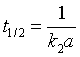 
，半衰期与反应物的初始浓度成反比；
3）反应速率系数k的量纲为
。
若二级反应只有一种反应物A，则速率方程的形式与上面相同，但应注意，此时式中的k2应为kA，并且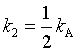
。
（2）反应物A、B的初始浓度不同（a≠b）
速率方程的微分式为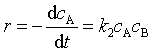 
速率方程的定积分式为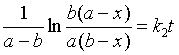 
浓度与时间的线性关系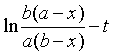 
半衰期 
3. 三级反应
反应速率与反应物浓度的三次方成正比的反应称为三级反应。例如 :
, 
，
若
（
、
、c分别A、B、C的起始浓度）
速率方程微分式为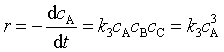 
速率方程定积分式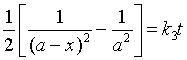 
浓度与时间的线性关系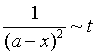 
半衰期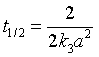 
式中k的量纲为
。
4. 零级反应
反应速率与物质浓度无关的反应称为零级反应.
速率方程微分式为: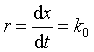 
（用产物浓度表示）
速率方程定积分式: 
＝k0t
浓度与时间的线性关系: 
半衰期: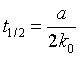 
式中k的量纲为
。
总之，对n级的简单反应（n≠1），起始浓度均相同时，速率方程定积分式为: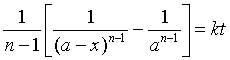
，
半衰期为A·
（A为常数），k的量纲为
。
5. 确定反应级数的方法
化学反应的级数需由实验确定。在掌握充分的实验数据的基础上，可以利用积分法、微分法、半衰期法以及孤立法等方法确定化学反应的反应级数。
（六）四种典型复合反应
1. 1-1级对峙反应
设
，
为生成物的浓度，
为平衡时生成物的浓度，K为平衡常数。
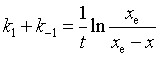
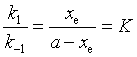
2. 一级平行反应
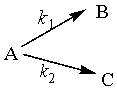
设
，t时刻B、C的浓度分别为
，则
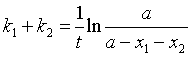
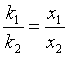
3. 1-1级连串反应
设
，t时刻A，B，C的浓度分别为
，则t时刻
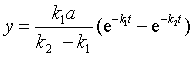
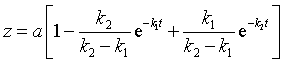
时刻，中间产物达最大值
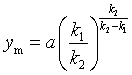
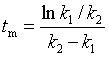
4. 链反应
根据链的传递方式的不同，可以将链反应分为直链反应和支链反应。直链反应分为链的引发、链的传递和链的终止三个阶段。在直链反应中主要学习如何对复杂的化学反应做最基本的动力学研究。支链反应容易引起爆炸，要特别注意可燃物的爆炸区间。
（七）反应速率与温度的关系
对于具有明确反应级数的化学反应，其反应速率系数与温度的关系服从阿伦尼乌斯公式。阿伦尼乌斯公式具有以下形式：
指数式: 
（式中
为活化能，A为指前参量。）
对数式: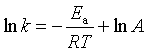 
微分式: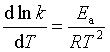 
定积分式: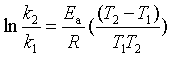 
（八）基元反应速率理论
1. 简单碰撞理论
（1）双分子气体反应的碰撞频率Z
同种分子 :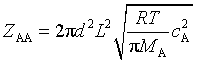
不同分子: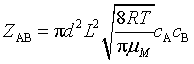 
,其中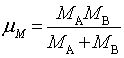 
（2）双分子气体反应速率
同种分子: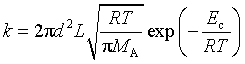
不同分子: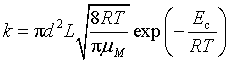
,其中
为阈能。
2. 过渡态理论（活化络合物理论）
对于双分子气相反应，
（1）以压力表示的反应速率系数
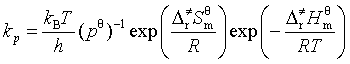
其中
为玻耳兹曼常量；h为普朗克常量；
为活化熵，
为话化焓。
（2）以浓度表示的反应速率系数
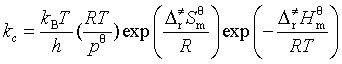
3. 各种活化能及其关系
（1）反应活化能
反应活化能是唯象宏观量。对于基元反应，将具有平均能量的反应物分子变成具有平均能量的活化分子所必须给予的能量，称为反应的活化能。
对于复合反应，活化能没有明确的物理意义，仅仅是组成复合反应的一系列基元反应活化能的组合，其组合方式取决于表观速率系数与基元反应速率系数之间的关系。
（2）阈能
是分子发生有效碰撞时，指定态反应所需的最低平动能。它与温度无关，是微观量。
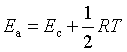
（3）能垒
是反应物形成活化络合物时，活化络合物最低能级与反应物最低能级的势能差。
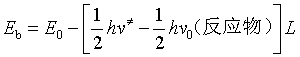
式中：
是活化络合物的零点能与反应物零点能之差。
（九）三种处理复合反应的近似方法
处理复合反应的近似方法有稳态近似法 、平衡假设法和选取速控步骤法.
二、 重点与难点
化学热力学是对反应平衡态的研究，而化学动力学是研究现实的反应系统，它的实质是研究反应过程随时间变化的规律性，即反应速率的表达、速率与浓度间的关系、各种因素对反应速率的影响以及探讨化学反应机理等。概括起来，化学动力学研究的主要内容是反应速率与反应机理。当然，随着科学技术的不断发展，还有更深入的内容，如微观反应动力学及动力学的其它分支内容等，但就基础而言，仍是反应速率和反应机理。
（一）反应速率
1. 反应速率方程
反应速率及速率方程式的表示：根据不同的研究需要，有平均速率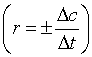
、瞬间速率（也称即时速率，
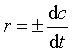）。研究反应的速率规律，不但要写出反应速率，还必须写出反应的速率方程式。
广义地说，表示反应速率与影响它的各种因素（如浓度、温度、溶剂、各种场…）的关系方程称反应速率方程，但实际上能同时包括各种因素的方程具体形式是很难表述的，在动力学所研究的速率方程中有
、
、
等各种形式，其中，在一定温度下化学反应速率与反应物浓度间关系的方程是研究的重点。
对基元反应，速率方程可以根据基元反应的质量作用定律来描述（即在恒定的温度下，基元反应的速率与所有反应物浓度的幂乘积成正比，其中幂指数恰是反应式中各相应物质的反应分子数）；对非基元反应，有的速率方程会很复杂，对某些化学反应，若是用实验方法来确定的速率方程称为“经验速率方程”，若是由反应机理推导出的速率方程称为“机理速率方程”。
除浓度外，在其他因素不变时，对于定温下反应速率与浓度间的速率方程
转化的浓度与时间的函数关系式
，也称“动力学方程”。
2. 反应级数
（1）反应级数可为正整数、分数、零或负数，但有些复合反应（如H2 + Br2 ==== 2HBr）的速率方程，反应速率与反应物浓度之间无简单的级数关系。必须注意，只有速率方程符合
…形式的反应才有反应级数可言。
（2）反应级数与反应分子数的区别：对于基元反应，反应级数为正整数且等于反应分子数。但有些反应的速率方程形式看起来符合质量作用定律，但它却不是基元反应（如H2+I2====2HI，其速率方程为
，它是复合反应），此时的反应级数就不能说是反应分子数。只有基元反应才具有反应分子数的概念。
（3）如何确定反应级数是动力学研究的一个重点，对宏观的化学反应而言，它需由实验来确定。可以用微分法、积分法、半衰期法、孤立法等等来确定。对于指定的化学反应,级数可因反应条件的变化而发生改变，如当反应过程中某些反应物的浓度变化极小或甚至不变时，可作为常数与速率系数合并（总反应级数称为“假级数”、“准级数”，如酯的水解、蔗糖在酸催化下水解等反应），对反应级数的确定有助于确定反应速率方程。
3. 反应速率理论
在反应速率理论中，接触及介绍最多的是阿伦尼乌斯理论、碰撞理论和过渡态理论。
阿伦尼乌斯理论建立了速率系数（k）与温度（T）的经验关系式，提出了活化状态及“活化能”（ 
）的概念。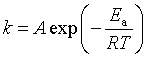
虽然是经验式，但阿伦尼乌斯理论却为其他的速率理论发展奠定了基础，许多动力学的问题，至今还需借助阿伦尼乌斯理论进行计算，从而解决实际问题。
碰撞理论从物质的微观运动出发解决碰撞频率的计算，同时认为只有相对碰撞动能大于一定值时，才能发生反应，将此能量界限引入速率计算，提出了“阈能”（ 
）的概念。
过渡状态理论从物质的微观结构及微观运动的观点出发，考虑在基元反应中粒子（质点）位能的变化，从而解决速率理论的计算问题，提出了“活化过渡状态”和“能垒”（ 
）的概念。
碰撞理论和过渡态理论虽比阿伦尼乌斯理论有进一步的发展，但尚未取得实质性的突破，目前应用最广的还是阿伦尼乌斯理论。碰撞理论与过渡状态理论的公式推导，最终都能与阿仑尼乌斯公式相关联，由此也有助于区别几种活化能之间的关系。
使用阿伦尼乌斯公式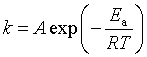
时须注意，它只代表一部分反应速率系数与温度的关系，有的反应规律是相反的（如升温时速率反而降低），或是特殊的（如随升温速率先升后降等）。
另外，关于对峙反应中，正逆反应活化能之差与反应热效应的问题：若反应时，系统的体积不发生变化，反应热效应为Qv = △U= E正－E逆（认为活化能是热力学能的一部分）；若将对峙基元反应的平衡常数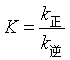
与等压方程共同考虑时，即在等压情况下，反应热效应为Qp = △H＝E正－E逆。
4. 影响反应速率的各种因素
（1）温度 研究温度对反应速率的影响应用最广泛的是阿伦尼乌斯公式，运用该公式的定积分形式，可以计算同一反应在不同温度下的速率系数，在实际中有很大用处。但阿伦尼斯理论认为活化能与温度无关，而事实上活化能与温度有关，精确的实验表明，在温度变化范围很小时，Ea与温度有关，在温度变化范围大时，
随温度的变化就更为明显。在一般要求不高的计算中，多数将
视为与温度无关的量，但精确计算，必须用到修正经验公式，即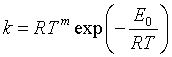
，其微分式为
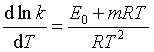；m和
都与温度无关，
，当
时，
。
（2）浓度 在固定温度的情况下，浓度对速率的影响表现在以
的速率方程中，在计算时，要变换成c = f(t) 形式的动力学方程。对基元反应，可直接根据质量作用定律写出速率方程，但对复杂反应就要先根据反应机理来确定速率方程，再进一步得到
的关系式。熟练掌握具有简单级数的化学反应（零级、一级、二级、三级）的动力学规律，熟记它们中
的关系，将有利于进行各种动力学过程的计算。
（3）催化作用 催化剂能改变化学反应速率而自身在反应前后的数量与化学性质都不发生变化。催化剂的作用是通过改变反应途径、降低反应活化能，从而改变化学反应的速率。 由于催化剂不能改变反应的
，故催化剂的加入也不能改变平衡常数。催化剂的用量一般很少，对多相催化反应，催化剂的存在不会改变反应系统的始、终状态，但对均相催化，加入催化剂会改变浓度，由于用量少，一般也忽略它对浓度的影响。实验证明催化剂还能改变指前参量，催化剂的存在能使反应的指前参量和活化能都减少，由于A和
对化学反应速率规律变化的影响是相反的，只有当活化能
的减少占优势时，催化剂才能加快反应速率。
（二）反应机理
1. 复合反应的动力学
实际的化学反应不但机理复杂，而且速率方程也呈现多样化。由于机理复杂，不少化学反应无法建立可靠的速率方程。目前对一些典型的复合反应可以进行动力学讨论，如对峙反应、平行反应、连串反应、某些链反应等等。
动力学处理的关键：讨论的关键是抓住反应机理，根据特点写出速率方程式，再整理化简，用
的动力学方程表征。
如对峙反应，无论是1-1、1-2、2-1、2-2型，其特点都是经过足够长时间达到平衡时，正、逆反应的速率相等，产物生成速率等于正反应速率和逆反应速率之差。据此来求解动力学方程。
又如平行反应，无论是一级还是二级，它的总反应速率等于同时进行各反应的速率之和，且推导得出的速率方程和动力学方程与同级的简单级数反应的速率方程和动力学方程类似。
对于连串反应，由于前一基元反应的产物是后一步基元反应的反应物，可根据基元反应的质量作用定律写出速率方程，并求解各种物质在t时刻的浓度。
对复杂动力学问题处理时常常用到稳态法和平衡近似法。用稳态法处理时必须符合反应迅速达到稳定态、活泼中间产物（一般为自由原子或自由基）的浓度比反应物及产物浓度都小得多，不能认为凡是活泼中间产物就可以用稳态法处理。用平衡近似法时，在复合反应中必须包括有能迅速达到化学平衡的可逆反应，其反应后存在的基元反应是慢反应（速率很小），是决速步骤。
2. 反应机理的确定
确定反应机理时要考虑速率、能量、结构三个方面的因素，在化学动力学基础学习中，一般只要求能利用化学反应历程推导出速率方程，求出活化能，并与实验结果相比较。必须指出，最终机理的确定还需要通过新的实验，包括对中间产物的定性、定量鉴定等。
进入你问我答
