一、电导、电导率、摩尔电导率

导体的导电能力可以用电导来表示，以符号G表示之，它是电阻R的倒数，即，其单位为西门子，符号为S，。

由于导体的电阻与其长度成正比，与截面积成反比，所以导体的电导与截面积A成正比，与长度l成反比，即

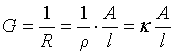                 (11)

式中k是比例系数，称为电导率，它是电阻率r的倒数，单位为。当导体的截面积，长度时，它的电导就是电导率。

对电解质溶液而言，将面积为1m²的两平行板电极置于电解质溶液中，两电极间的距离为1m时的电导即为该溶液的电导率。电解质溶液的电导率数值与电解质的种类、溶液浓度及温度等因素有关。

在表达电解质溶液的导电能力时，还常使用摩尔电导率。摩尔电导率为溶液的电导率与其物质的量浓度之比，即单位浓度溶液的电导率。表示为

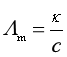                 (12)

的单位为。

在表示电解质的摩尔电导率时，必须标明基本单元，否则摩尔电导率的物理意义不明确。例如，同一溶液，由于，所以。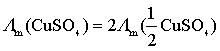

二、电解质溶液的电导的测定及电导率和摩尔电导率的计算

 

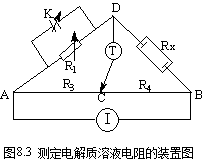
电导是电阻的倒数，因此，测量电解质溶液的电导，实际是测量其电阻。测量溶液的电阻，可利用惠斯顿电桥，图8.3为测量装置示意图。图中电源I使用的是低频交流电(通常取其频率为1000Hz)，不能使用直流电，因为直流电通过电解质溶液时会发生电解而使电极附近溶液浓度发生改变，并可能在电极上析出物质而改变电极的本质；AB为均匀的滑线电阻；R₁为可变电阻箱；R₃、R₄分别为AC、CB段的电阻；R_x为盛有待测溶液的电导池的电阻，该电导池的两电极一般用镀有铂黑的铂片制成；K为用以抵销电导池电容的可变电容器；T为检零器，一般为示波器或耳机。测定时，接通电源，选择一定的电阻R₁，移动接触点C，直至CD间的电流为零。这时，电桥平衡，R₁ R₄= R₃ R_x，故溶液的电导为

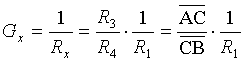                        (13)

因此，再结合式(9)可得待测溶液的电导率为

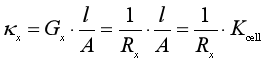                     (14)

对于一个固定的电导池，l和A都是定值，故比值为一常数，称此常数为电导池常数，用符号表示，单位为m^-1。

通常，将一个电导率已知的电解质溶液注入该电导池中，测其电阻，根据式(12)计算之值。测知此电导池的电导池常数后，再将待测溶液注入此电导池中，测其电阻，即可由式(14)求出待测溶液的电导率，再根据式(12)可计算其摩尔电导率。

用来测量电导池常数的电解质溶液通常为KCl水溶液，其电导率可从文献中查到，表3列出了298.15K下不同浓度KCl水溶液的电导率。
               表3  298.15K时一些浓度的KCl水溶液的电导率

例4  已知18℃时0.02 molKCl水溶液的电导率k= 0.2397S。在18℃时，以某电导池分别充以0.02 mol的KCl水溶液和0.0014083 mol的NaCNS酒精溶液时，测得的电阻分别为15.946W和663.45W。试求算：(1)电导池常数；(2)该NaCNS酒精溶液的摩尔电导率。

解  (1)根据式(8.12)，该电导池常数为

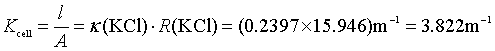
(2)根据式(8.12)，0.0014083 mol的NaCNS酒精溶液的电导率为

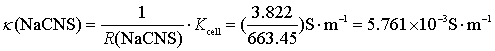
所以   

三、电导率、摩尔电导率与浓度的关系

电解质溶液的电导率、摩尔电导率均与浓度有关，但强、弱电解质所表现出的规律不尽相同。

图8.4给出了几种不同电解质的电导率k随浓度变化的曲线。由图可以看出，强电解质溶液的电导率k先随浓度的增大而增加，当浓度增大到一定程度后，由于阴、阳离子之间的相互吸引明显增大，因而使离子的移动速度下降，电导率反而下降，所以在电导率与浓度的关系曲线上会出现最高点。对弱电解质而言，电导率k虽然也随浓度的增大有所增加，但变化并不明显。这是因为浓度增大时，虽然单位体积中电解质分子数增加了，但电离度却随之减小，溶液中离子数目变化并不显著所至。

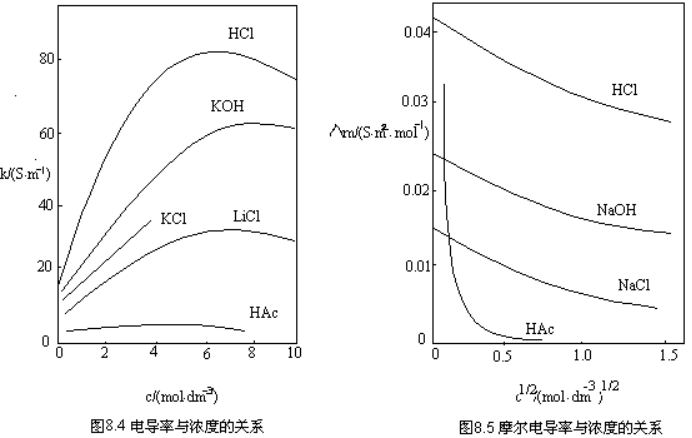
摩尔电导率随浓度的变化与电导率的变化不同，图8.5给出了一些电解质的摩尔电导率随浓度变化的曲线。由图可以看出，无论是强电解质还是弱电解质，溶液的摩尔电导率均随浓度的增大而减小，这是因为溶液的浓度降低时，离子间吸引力减弱，离子运动速度增加，故摩尔电导率增大。但强、弱电解质的变化的规律也是不同的。对强电解质而言，科尔劳施(Kohlrausch)总结了大量实验结果，得出了如下结论：在浓度极稀的溶液中(通常c< 0.001mol)，强电解质溶液的摩尔电导率与浓度的平方根成线性关系，用公式表示为

                      (15)

式中b在一定温度下对一定的电解质和溶剂而言是一个常数，为无限稀释时电解质溶液的摩尔电导率，又称为极限摩尔电导率。可见，强电解质溶液的极限摩尔电导率可用与的线性关系外推至而求得。

对弱电解质来说，随着溶液浓度降低，弱电解质的解离度增大，摩尔电导率也有所增加。当溶液浓度极稀时，电解质几乎全部解离，离子数目剧增，因此摩尔电导率急剧增大。与c之间不存在如式(15)的简单关系，即使在浓度极稀时，摩尔电导率仍与相差甚远，故弱电解质无限稀释时的摩尔电导率不能用外推法求得。

那么，如何求算弱电解质无限稀释时的摩尔电导率呢？科尔劳施的离子独立移动定律解决了这一问题。

四、离子独立移动定律和离子的摩尔电导率

依据强电解质溶液在无限稀释时的摩尔电导率(用外推法求得)的大量实验数据，科尔劳施总结得出离子独立移动定律：在无限稀释时，所有电解质都全部电离，且离子间一切相互作用均可忽略，离子在电场作用下的移动速度只取决于该离子的本性，而与共存的其它离子的性质无关。因此，电解质溶液无限稀释时的摩尔电导率应为阴、阳离子的无限稀释摩尔电导率、之和。即对电解质，无论是强电解质还是弱电解质都有下列关系式：

                    (16)

式中，、分别为阳离子、阴离子的化学计量数，此式称为科尔劳施离子独立移动定律。

根据上述定律，可以利用有关强电解质的计算出弱电解质的。例如，

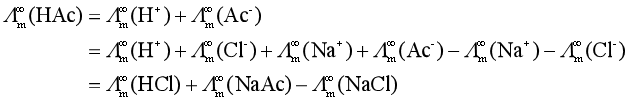
很显然，若能得知各种离子的无限稀释摩尔电导率，则可直接用式(8.16)计算无限稀释时电解质的摩尔电导率。

离子的无限稀释摩尔电导率可以由离子的迁移数求得。电解质的摩尔电导率是阴、阳离子摩尔电导率贡献的总和，所以离子的迁移数也可以看作是某种离子的离子摩尔电导率占电解质的摩尔电导率的分数，在无限稀释时，有

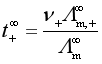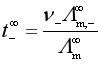    ，                   (17)

可见，利用实验求得的电解质的和该电解质的和，即可求得离子的无限稀释摩尔电导率和。

离子的无限稀释摩尔电导率也可以由无限稀释溶液中离子的电迁移率求得。设在浓度为c的电解质溶液中，放入两面积为A的金属电极，两电极间的垂直距离为l，电势差为E，并设溶液中电场是均匀的。

由式(7)可知通过溶液的电流强度为

用离子的电迁移率代替离子迁移速率得

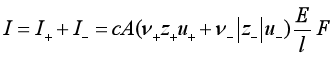              (18)

引入摩尔电导率，并利用欧姆定律可得

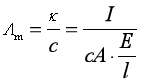                      (19)

将式(18)代入上式得

                   (20)

在溶液无限稀释时，离子的电迁移率分别为、，因此上式变为

                  (21)

与式(16)比较，可得

  ，                    (22)

表4列出了298.15K下一些常见离子在无限稀释的水溶液中的摩尔电导率。

     表4  298.15K下无限稀释的水溶液中一些常见离子的无限稀释摩尔电导率

从表4可以看出，在水溶液中，H⁺和OH^－的无限稀释摩尔电导率特别大。一般认为并不是质子本身的迁移，而是溶剂化的质子在水分子间转移，导致电流很快沿着氢键被传导；或质子从水分子上转移到OH^－离子上，类似于OH^－的反方向运动。H⁺和OH^－的这种异常现象只有在水溶液中或含有OH基的溶剂(如ROH)中显现。

对于浓度不大的强电解质，可近似有下列关系：

，

，  

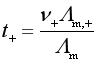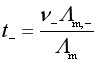
t₊、t_－及都可由实验测得，从而可计算出实际浓度的强电解质溶液中离子的摩尔电导率。

例5  有一电导池，其电极的有效面积为2cm2，电极之间的有效距离为10cm，在池中充以1—1价型的盐MX的溶液，浓度为0.03mol·dm^-3，用电位差为3V，电流强度为0.003A的电流通电。已知M⁺离子的迁移数为0.4，试求：

（1）MX的摩尔电导率。

（2）M⁺和X^－离子的摩尔电导率。

（3）在这种实验条件下M⁺离子的移动速度。

解 （1）由式(8.19)可知

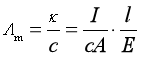
则     Λ_m(MX) =[0.003×(10×10^-2)/(0.03×10³)×(2×10^-4)×3]

=1.67×10^-2 

(2)   Λ_m (M⁺)=t_M⁺·Λ_m(MX)

=(0.4×1.67×10^-2)

=6.68×10^-3

Λ_m (X^-)=t_X-·Λ_m(MX)

=(0.6×1.67×10^-2)

=1.00×10^-2

（3） r₊=u₊(dE/dl)=[Λ_m(M⁺)/F]·(E/l)

=[(6.68×10^-3/96500)×(3/0.1)]m·s^-1

=2.07×10^-6 m·s^-1

五、电导测定的一些应用

1．测定弱电解质的解离度α及解离平衡常数

对于弱电解质，由于解离度较小，溶液中离子的浓度不大，可以认为离子的移动速度受浓度的影响很小，故可以假定： ， ，这样

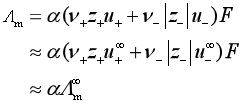
式中为弱电解质浓度为c时的摩尔电导率，为该电解质的无限稀释摩尔电导率。因此，该弱电解质的解离度为：

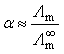                       (23)

若电解质为1-1价型或2-2价型，则此时弱电解质化学式为，其解离平衡常数为：

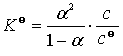
将式(23)代入上式后整理可得

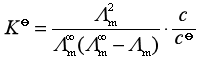              (24)

该式称为奥斯特瓦尔德稀释定律。

例6  298K时将电导率为0.141S·m^-1的KCl溶液装进电导池，测得电阻为525Ω，在该电导池中若装进0.1mol·dm^-3的NH₄OH溶液，测出电阻为2030Ω，计算此NH₄OH溶液的解离度及解离平衡常数。

解  因为 (NH₄OH)= (NH₄⁺) +(OH^－)

=(73.4+198.0)×10^-4S·m²·mol^-1

=2.714×10^-2S·m²·mol^-1

而  K_cell=k(KCl)R(KCl)=(0.141×525) m^-1=74.03m^-1

则  k (NH₄OH)=K_cell/R(NH₄OH)=(74.03/2030)S·m^-1=0.03647S·m^-1

Λ_m=k (NH₄OH)/c(NH₄OH)

= [0.03647/(0.1×10³)] S·m²·mol^-1

=3.647×10^-4S·m²·mol^-1

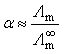= 3.647×10^-4/(2.714×10^-2)

= 0.01344

所以 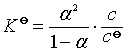 =1.0×(0.01344)² /(1－0.01344)=1.83×10^-5

2．测定难溶盐的溶解度

难溶盐如BaSO₄、AgCl等在水中的溶解度很小，其在水中的浓度难以用普通的滴定方法测定，但可用电导法测得。

对于难溶盐的电解质溶液，由于溶液很稀，水的电导率对整个电解质溶液的电导率的贡献已不可忽略，所以，必需扣除水的电导率，即

                (25)

又由于溶解度很小，溶液中离子的浓度很低，可用认为

                  (26)

这样，再利用公式(12)计算得难溶盐的饱和溶液的浓度，从而求得难溶盐的溶解度。

例7  298K时测得SrSO₄饱和水溶液的电导率为1.482×10^-2S·m^-1，该温度时所用水的电导率为1.5×10^-4S·m^-1。试计算该条件下SrSO₄在水中的溶解度。

解  因为(SrSO₄)= (Sr²⁺)＋(SO₄^2-)

= (5.946＋7.98)×10^-3S·m²·mol^-1

= 1.393×10^-2S·m²·mol^-1

则     (SrSO₄)=2(SrSO₄)=2.786×10^-2S·m²·mol^-1

而      k (SrSO₄)=k (溶液)－k (H₂O)

= (1.482×10^-2－1.5×10^-4)S·m^-1

= 1.467×10^-2S·m^-1

所以     c(SrSO₄)=k (SrSO₄)/(SrSO₄)

= [1.467×10^-2/(2.786×10^-2)] mol·m^-3

= 5.266×10^-1mol·m^-3

由于该饱和水溶液浓度很小，该溶液的密度与溶剂水的密度近似相等，因此

c(SrSO₄)=5.266×10^-4mol·kg^-1

所以SrSO₄的溶解度为

S = c(SrSO₄)×M(SrSO₄)

= (5.266×10^-4×183.7×10^-3)kg·kg^-1

= 9.67×10^-5 kg·kg^-1

3．电导滴定

电导滴定将分析化学中的滴定与电导测定相结合，利用滴定过程中溶液的电导的变化转折确定滴定终点。该法常被用来测定电解质的浓度，尤其是当溶液有颜色或浑浊而无法应用指示剂时，此法就更为方便、有效。该方法可用于酸碱中和、生成沉淀、氧化还原等各类滴定反应。

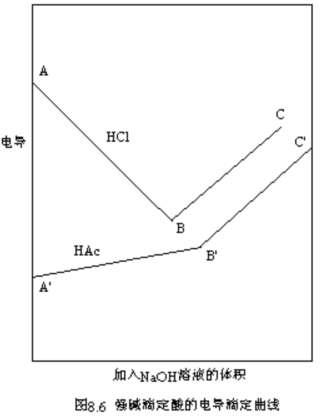
通常被滴定溶液中的一种离子与滴入试剂中的一种离子相结合，生成解离度极小的弱电解质或沉淀，使溶液中原有的一种离子被另一种离子替代，溶液的电导发生改变。以酸碱中和滴定为例，强碱滴定强酸时，如NaOH溶液滴定HCl溶液，溶液中电导率很大的H⁺被电导率较小的Na⁺取代，因此溶液的电导随着NaOH溶液的不断加入而逐渐变小。当HCl被中和后，再加入NaOH，则相对于净增加溶液中的Na⁺及OH^－，由于OH^－的电导率也很大，所以溶液的电导又增加。将溶液的电导对所加入的NaOH溶液的体积作图，则可得图8.6中的AB和BC两条直线，它们的交点B就是滴定终点。强碱滴定弱酸时，如NaOH溶液滴定HAc溶液，由于HAc为弱酸，电导率很小，随着NaOH的加入，弱酸逐渐被完全解离的盐NaAc所代替，因此溶液的电导率逐渐增加(如图8.6中的段)。当HAc被中和后，再加入NaOH，则相当于净增加溶液中的Na⁺及OH^－，所以溶液的电导迅速增大(如图8.6中的段)。和两条直线的交点就是滴定终点。

可见，电导滴定与使用指示剂的滴定不同，它无需过分关心终点是否达到或超过，只需在终点两边作几次测定，就可得到电导滴定直线，从而得到准确的滴定终点。