一、比表面

多相分散系统的分散程度通常用比表面a_s来表示，其定义为
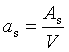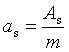      或     (1)

A_s代表体积为V（或质量为m）的物质所具有的表面积。所以比表面a_s是单位体积（或质量）的物质所具有的表面积，其数值随着物质分散程度的增加而显著增大。当1cm³的物质被分散到颗粒大小为0.1μm-1nm时，其表面积可达60—6000cm²，对于这样的高分散多相系统，界面性质对整个系统性质的影响是非常显著的。

 

二、表面吉布斯自由能和表面张力

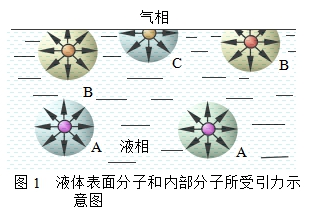
对于凝聚相而言，表面层分子与内部分子的受力情况是不同的。图1表示液体表面分子及体相内部分子的受力情况，球半径表示分子所受的引力范围。液体内部的分子A受到周围分子的引力是对称的，其合力为零。但靠近表面的分子B及表面上的分子C则与A不同，液体内部密集的液体分子对它们的引力远大于上方稀疏的气体分子对它们的引力，分子所受作用力的合力垂直于液面而指向液体内部，即表面分子受到指向液体内部的拉力，通常称作净吸力。因此，在没有其它作用力存在时，所有液体都有缩小表面积的趋势。而要扩展液体的表面，即把一部分分子由内部移到表面上来，则需要克服净吸力而消耗功（即环境对系统做功），所消耗的功全部或部分转变成表面分子的势能。可见，表面分子比内部分子具有更高的能量。
   在一定的温度和压力下，对一定的液体而言，扩展表面所需消耗的功δW'应与增加的表面积dA成正比。设比例系数为γ，则有

                           (2）

δW'表示环境对系统做的功，称为表面功。当表面积增加时，dA_s＞０，δW'＞０，即环境做正功；当表面积减小时，dA_s＜０，δW'＜０，即系统做正功。
  若在定温定压下可逆地增加表面积，则dG ＝δW'，即可逆地增加表面积所消耗的功，等于系统表面Gibbs自由能的增加，此时有
                              (3)

dG表示新增加的dA_s表面层分子比相同数量的内部分子多出的吉布斯自由能。
  由式（3）可知，若dA_s＜０，则dG＜０，即表面积减小的过程是自发变化。两个小液滴接触会逐渐变成一个大液滴，乳状液静置后会自动分层，都是自动缩小表面积、降低系统自由能的自发变化。
  式（3）又可改写作
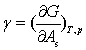                              (4)
  可见，γ的物理意义是：定温定压下增加单位表面积所引起的系统吉布斯自由能的变化，即单位表面的分子比相同数量的内部分子多余的吉布斯自由能。称γ为比表面吉布斯自由能，简称为表面自由能，其单位为J·m^-2。
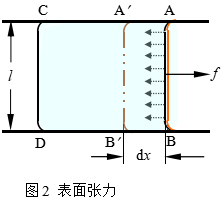
  我们还可以从另外一个角度讨论γ的物理意义：由于表面分子在微观上受到与液面垂直、指向液体内部的净吸力，因而表面层分子有进入液体内部的倾向，在宏观上表现为有一个与表面平行，力图使表面收缩的力。例如：用细铁丝做成一个一边可以滑动的方框（图2），将铁丝框浸入肥皂液中使框表面形成一层肥皂膜。将铁丝框取出后，能观察到肥皂膜会自动收缩，并带动AB边向CD方向滑动，这说明肥皂膜表面具有自动收缩的力。

若将金属丝AB从虚线位置A’B’向右移动 dx，使肥皂膜表面积增大dA_s＝２ldx（肥皂膜有两个面），则需施加一外力f对系统做功δW'，

即

        

此功即为表面功，因而有

        

整理后可得

        

可见，γ就是与表面平行，垂直作用于单位长度上的使表面收缩的力，我们称之为表面张力，其单位为N·m^-1。

        

综上所述，γ既是表面自由能，又是表面张力，二者数值相等，单位可以相互转换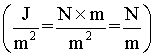。它们都是系统的强度性质，其数值与物质的本性、共存另一相的性质以及温度、压力等因素有关。通常在讨论界面热力学时，γ当作表面自由能使用，在讨论界面间的相互作用及平衡关系时，γ当作表面张力使用。
  一些纯液体在常压、293.2K时的表面张力列于表1。对于纯液体来说，共存另一相一般指饱和蒸气或饱和了本身蒸气的空气。如果共存的另一相发生变化，则表面张力值也会有很大的变化。表2列出了汞和水与不同物质接触时的界面张力。

            表1  293.2K常压下某些液体的表面张力

液    体	γ/mN.m	液    体	γ/mN.m
水 苯 甲    苯 乙    醇 丙    酮	72.8 28.9 28.4 22.3 23.7	甲    醇 乙    醚 硝 基 苯 二硫化碳 四氯化碳	22.6 16.9 41.8 33.5 26.9

表2  293.2K常压下汞或水与不同物质接触时的界面张力

第一相	第二相	γ/mN.m	第一相	第二相	γ/mN.m
汞 汞 汞 汞	汞蒸气 乙  醇 水 苯	471 364 375 362	水 水 水 水	水蒸气 正庚烷 苯 丁  醇	72.8 50.2 32.6 1.76

升高温度时，一般液体的表面张力都降低。这是因为升温时液体分子间距离增大，引力减小，而与之共存的蒸气密度加大，对液体表面分子的作用力增强，致使表面分子受到的净吸力减小，因而表面分子的过剩吉布斯自由能减少。当达到临界温度时，气、液不分，表面张力降低至零。

固体表面分子与液体一样，也具有过剩吉布斯的自由能，但到目前为止，还不能直接用实验方法测定固体的表面张力，根据间接推算，固体的表面张力比液体的要大得多。

三、界面的热力学性质

对于组成不变的系统，当有表面功存在时，各热力学函数变化的关系式应为

，当S、V一定时，；

，当S、p一定时，；

，当T、V一定时，；

，当T、p一定时，。

由以上四式可得

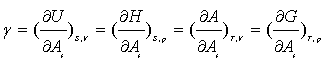      (5)

可见，γ是在指定相应变数的条件下，每增加单位表面积时，系统的热力学函数的增量。

当V一定时，，由此可得

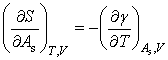                 (6)

同理，p一定时，，可得

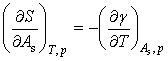                 (7)

由dU和dH的表达式可得

      

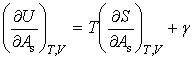
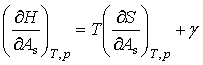
将式(6)和式(7)分别代入以上两式得

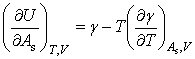                (8)

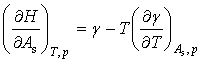                (9)

由于表面张力随温度升高而降低，即 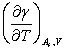和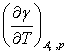均小于零，所以由式(5)－(9)可知，增大表面积时，系统的熵、热力学能及焓都增加，它们的增量可以通过表面张力及其随温度的变化关系进行计算。

例1  293.2K，p^ө下，将半径r₁=1.00x10^-3m的水滴分散成半径r₂=1.00x10^-9m的小水滴，试计算分散后小水滴的数目及表面吉布斯自由能的变化。已知该温度水的表面张力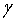= 0.0728N·m^-1。

解 设小水滴的数目为N，则
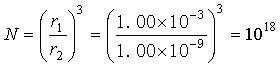