二、时间数列水平分析
　1．发展水平与平均发展水平
　　,……， 称为最初水平，称为最末水平，也可表示为,,…… ， 为基期水平，为报告期水平。

　　平均发展水平是现象在时间上的取值的平均数，又称为序时平均数。

　　（1）绝对数时间数列的序时平均数
　　时期数列
　　时点数列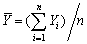

【例】求全年平均库存。
　　

分析：
　　如果一季初到一季末库存变化均匀，则一季度平均库存为：
　　一季平均库存：　　以此类推
　　二季平均库存：
　　三季平均库存：
　　四季平均库存：
　　全年平均库存：
　　如果按算术平均法计算（不合理）
　　

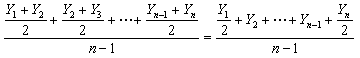
　　间隔不等条件下


【例】
　　
　　1-2月平均人数：
　　3-6月平均人数：
　　7-9月平均人数：
　　10-12月平均人数：
　　全年平均人数：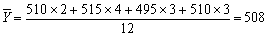
　　把间隔作为权数：
　　

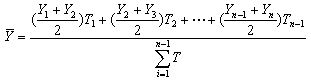
　　（2）相对数（平均数）时间数列序时平均数
　　观察值
　　先求，然后：
【例】某厂1995-1996年各月工人人数资料如下：
　　
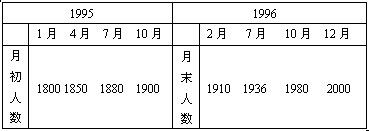
　　并知1995年末人数为1900人，1996年工业总产值为3679万元，试计算：
　（1）1995年和1996年的月平均工人数
　（2）1996年的月平均劳动生产率

解：
　（1）
　　　　
　　　
　　　　　

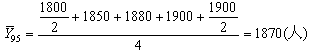
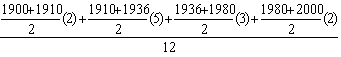
　（2）b代表工业总产值Y代表劳动生产率，a代表工人数

　　　
　　　故：


　2.增长量与平均增长量
　　（1）增长量：
　　增长量是时间数列中不同时期的发展水平之差，用于描述现象在观察期内增长的绝对数量。

　　基本式： 增长量=报告期水平－基期水平

　　由于基期不同，又可分为逐期增长量和累积增长量。

　　

　　逐期增长量之和等于累积增长量
　　

　　（2）平均增长量
　　平均增长量