内容导入：
用计算机进行的数值计算，由于受到计算机字长的限制，要求输入的数有一定的位数，计算的结果也只保留一定的位数，且所保留下来的不一定都是有效数字，同时也不是所有的有效数字都可保留下来。
教师解析：
在表示一个近似值时，为了同时反映其准确程度，常常用到“有效数字”的概念。
内容简介
1、有效数字的概念；
2、有效数字与误差的关系。
边学边练
取3.14，3.15，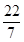
，
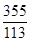作为π的近似值，求各自的绝对误差，相对误差和有效数字的位数。
分析：求绝对误差的方法是按定义直接计算。求相对误差的一般方法是先求出绝对误差再按定义式计算。注意，不应先求相对误差再求绝对误差。有效数字位数可以根据定义来求，即先由绝对误差确定近似数的绝对误差不超过那一位的半个单位，再确定有效数的末位是哪一位，进一步确定有效数字和有效数位。有了定理2后，可以根据定理2更规范地解答。根据定理2，首先要将数值转化为科学记数形式，然后解答。
解：（1）绝对误差:
e(x)=π－3.14＝3.14159265…－3.14＝0.00159…≈0.0016。
相对误差：
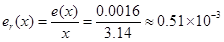
有效数字：
因为π＝3.14159265…=0.314159265…×10，3.14＝0.314×10，m=1。
而π－3.14＝3.14159265…－3.14＝0.00159…
所以│π－3.14│＝0.00159…≤0.005=0.5×10－2＝
所以，3.14作为π的近似值有3个有效数字。
（2）绝对误差:
e(x)=π－3.15＝3.14159265…－3.14＝－0.008407…≈－0.0085。
相对误差：
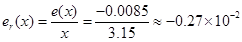
有效数字：
因为π＝3.14159265…=0.314159265…×10，3.15＝0.315×10，m=1。
而π－3.15＝3.14159265…－3.15＝－0.008407…
所以│π－3.15│＝0.008407……≤0.05=0.5×10－1＝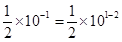
所以，3.15作为π的近似值有2个有效数字。
（3）绝对误差:
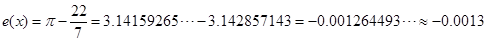
相对误差：
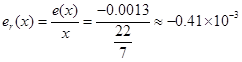
有效数字：
因为π＝3.14159265…=0.314159265…×10，
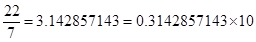，m=1。
而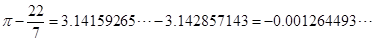
所以
所以，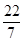
作为π的近似值有3个有效数字。
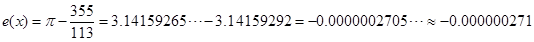（4）绝对误差:
相对误差：
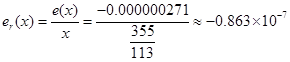
有效数字：
因为π＝3.14159265…=0.314159265…×10，
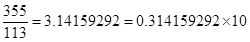，m=1。
而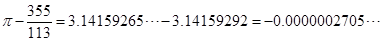
所以
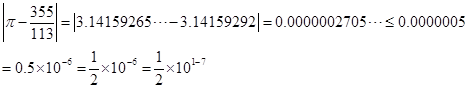
所以，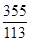
作为π的近似值有7个有效数字。
视频学习资源下载