知识点一:误差的种类及其来源
§1 引言
利用计算器、电子计算机等计算工具来求出数学问题的数值解得全过程,被称为数值计算。
随着科学技术的突飞猛进,无论是工农业生产还是国防尖端技术,例如机电产品的设计、气象预报和新型尖端武器的研制、火箭的发射等,都有大量复杂的数值计算问题亟待解决。它们的复杂程度已达到非人工手算(包括使用计算器等简单的计算工具)所能解决的地步。数字电子计算机的出现和飞速发展大大推动了数值计算方法进步,许多复杂的数值计算问题现在都可以通过电算(即用电子计算机进行数值计算)得到妥善的解决。
用数值计算的方法来解决工程实际和科学技术中的具体技术问题时,首先必须将具体问题抽象为数学问题,即建立起能描述并等价代替该实际问题的数学模型,例如各种微分方程、积分方程、代数方程等,然后选择合适的计算方法(算法), 编制出计算机程序,最后上机调试并进行运算,以得出所欲求解的结果来。
所谓数值计算方法,是指将所欲求解的数学模型(数学问题)简化成一系列算术运算和逻辑运算,以便在计算机上求出问题的数值解,并对算法的收敛性、稳定性和误差进行分析、计算。这里所说的“算法”,不只是单纯的数学公式,而且是指由基本运算和运算顺序的规定所组成的整个解题方案和步骤。一般可以通过框图(流程图)来较直观地描述算法的全貌。
选定合适的算法是整个数值计算中非常重要的一环。例如,当计算多项式
![]()
的值时,若直接计算![]() 再逐项相加,共需要做
再逐项相加,共需要做
![]()
![]()
次乘法和![]() 次加法。如当
次加法。如当![]() 时,需要做55次乘法和10次加法。若用著名的秦九韶(我国宋朝著名数学家)算法,将多项式P(x)改写成
时,需要做55次乘法和10次加法。若用著名的秦九韶(我国宋朝著名数学家)算法,将多项式P(x)改写成
![]()
来计算时,只要做![]() 次乘方和
次乘方和![]() 次加法即可。如当
次加法即可。如当![]() 时,只要做10次乘法和10加法。可见算法的优劣直接影响计算的速度和效率。
时,只要做10次乘法和10加法。可见算法的优劣直接影响计算的速度和效率。
对于小型问题,计算的速度与占用计算机内存的多寡似乎意义不大。但对复杂的大型问题而言,却起着决定性作用。
算法选得不恰当,不仅影响到计算的速度和效率,还会由于计算机计算的近似性和误差的传播、积累直接影响到计算结果的精度,有时甚至直接影响到计算的成败。不合适的算法会导致计算误差达到不能容许的地步,而使计算最终失败,这就是算法的数值稳定性问题。
数值计算过程中会出现各种误差,它们可以分为两大类:一类是由于算题者在工作中的粗心大意而产生的,例如笔误将886误写成868,以及误用公式等,这类误差称为过失误差或疏忽误差。它完全是人为造成的,只要在工作中仔细、谨慎,是完全可以避免的,我们就不再讨论它。另一类为非过失误差,在数值计算中则往往是无法避免的,例如近似值带来的误差,还有模型误差、观测误差、截断误差和舍入误差等。对于它们,应该设法尽量降低其数值,尤其是控制住经多次运算后误差的积累,以确保计算结果的精度。
下面通过一个简单的算例,可以看出近似值带来的误差和算法的选择对计算结果的精度所产生的巨大影响。例如,要计算
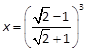
可用下列四种算式算出:
![]()
![]()
![]()
![]()
如分别用近似值![]() 和
和![]() …,按上列四种算法计算
…,按上列四种算法计算![]() 值,其结果如表1-1所示。
值,其结果如表1-1所示。
由表1-1可见,按不同算式和近似值所算出的结果五花八门、各不相同。有的甚至相差至巨,还出现了负值,这真是差之毫厘,谬以千里。可见近似值和算法的选定对计算结果的精确度影响很大。当然,此刻我们还不能说出表1-1中哪个计算更接近于![]() 的真值,这要在本章的§5中经过误差估计和分析后才能得到正确的结论。
的真值,这要在本章的§5中经过误差估计和分析后才能得到正确的结论。
因此,在研究算法的同时,还必须正确掌握误差的基本概念,误差在近似值运算中的传播规律,误差分析、估计的基本方法和算法的数值稳定性概念。否则,一个合理的算法也可能会得出一个错误的结果来。
表1-1
| 序号 | 算 式 |
计 算 结 果 |
|
|
|
||
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
§2 误差的种类及其来源
如上节所述,除了可以避免的过失误差外,还有不少无法避免的非过失误差存在于数值计算过程中,按照他们来源的不同,分述如后。
2.1 模型误差
在建模(建立数学模型)过程中,欲将复杂的物理现象抽象、归结为数学模型,往往只得忽略一些次要因素的影响,而对问题作某些必要的简化。这样建立起来的数学模型实际上必定只是所研究的复杂客观现象的一种近似的描述,它与真正客观存在的实际问题之间有一定的差别,这种误差称为模型误差。
2.2 观测误差
在建模和具体运算过程中所用的一切初始数据往往都是通过人们实际观察、测量得来的。由于受到所用观测仪器、设备精度的限制,这些测得的数据都只能是近似的,即存在着误差,这种误差称为观测误差或初值误差。
2.3 截断误差
在不少数值运算中常遇到超越运算,如微分、积分和无穷级数求和等,它们需用极限或无穷过程求得。然而计算机却只能完成有限次算术运算和逻辑运算,因此需将解题过程化为一系列有限的算术运算和逻辑运算。这样就要对某种无穷过程进行“截断”,即仅保留无穷过程的前段有限序列而舍弃它的后段。这就带来了误差,称它为截断误差或方法误差。例如,函数![]() 和
和![]() 可分别展开为无穷幂级数:
可分别展开为无穷幂级数:
![]() (1.2.1)
(1.2.1)
![]()
![]() (1.2.2)
(1.2.2)
若取级数的起始若干项的部分和作为![]() 时函数值的近似计算公式,例如取
时函数值的近似计算公式,例如取
![]() (1.2.3)
(1.2.3)
![]() (1.2.4)
(1.2.4)
则由于它们的第四项和以后各项都舍弃了,自然产生了误差。这就是由于截断了无穷级数自第四项起的后端而产生的截断误差。
式(1.2.3)和(1.2.4)的截断误差是很容易估算的,因为幂级数式(1.2.1)和(1.2.2)都是交错级数,当![]() 时各项的绝对值又都是递减的,因此,这是它们的截断误差
时各项的绝对值又都是递减的,因此,这是它们的截断误差![]() 可分别估计为
可分别估计为
![]()
和
![]()
2.4 舍入误差
在数值计算过程中还会用到一些无穷小数,例如无理数和有理数中某些分数化出的无限循环小数,如
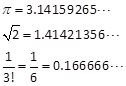
等。而计算机受机器字长的限制,它所能表示的数据只能有一定的有限位数,这时就需把数据按四舍五入舍入成一定位数的近似的有理数来代替。由此引起的误差称为舍入误差或凑整误差。
综上所述,在数值计算中除了可以完全避免的过失误差外,还存在难以回避的模型误差、观测误差、截断误差和舍入误差。数学模型一旦建立,进入具体计算时所要考虑和分析的就是截断误差和舍入误差了。在计算机上经过千百万次运算后所积累起来的总误差不容忽视,有时可能会大得惊人,甚至到达“淹没”所欲求解的真值的地步,而使计算结果失去根本的意义。因此,本书在以后各章讲解各种算法时,将对其截断误差的估算和舍入误差的控制作适当的介绍。
