§4  有效数字及其与误差的关系

4.1   有效数字

在表示一个近似值时，为了同时反映其准确程度，常常用到“有效数字”的概念。例如，对无穷小数或循环小数，可用四舍五入的办法取其近似值。，若按四舍五入取四位小数，则得的近似值为3.1416；若取五位小数，则得其近似值为3.14159.这种近似值取法的特点是误差限为其末位的半个单位，即

当近似值的误差限是其某一位上的半个单位时，我们就称其“准确”到这一位，且从该位起直到前面第一位非零数字为止的所有数字都称为有效数字。

一般说，设有一个数x，其近似值的规格化形式：

                                （1.4.1）

式中：都是中的一个数字，是正整数；是整数。

若的误差限为

                               （1.4.2）

则称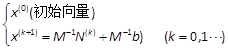为具有n位有效数字的有效数，或称它精确到。其中每一位数字都是的有效数字。若式（1.4.1）中的是经四舍五入得到的近似数，则具有位有效数字。例如，3.1416是的具有五位有效数字的近似值，它精确到0.0001。这样，203和0.0203都是具有三位有效数字的有效数。但要注意，0.0203和0.020300就不同了，前者仅具有三位有效数字，即仅精确到0.0001；而后者则具有五位有效数字，即精确到0.000001。可见，两者的精确程度大小不同，后者远较前者精确（差100倍）。因此，有效数尾部的零不可随意省去，以免损失精度。

另一种情况，例如，。这时的误差其绝对值超过了0.0005（第三位小数的半个单位），但却没有超过0.005（第二位小数的半个单位），即

显然，虽有三位小数但却只精确到第二位小数，因此，它只具有二位有效数字。其中都是准确数字，而第三位数字就不再是准确数字了，我们就称它为存疑数字。

还应注意，具有位有效数字的有效数虽是真值的准确到第位的近似值，但这第位数字有可能与真值中的同一位数字不相同。如不相同时，两者相差1。例如，3.1416是的准确到小数点后第四位的近似值，但它的末位数字是6，与真值中的小数点后的第四位数字5不同，两者相差1。

用计算机进行的数值计算，由于受到计算机字长的限制，要求输入的数有一定的位数，计算的结果也只保留一定的位数，且所保留下来的不一定都是有效数字，同时也不是所有的有效数字都可保留下来。

4.2 有效数字与误差的关系

由式（1.4.2）可知，从有效数字可以算出近似数的绝对误差限；有效数字的位数越多，其绝对误差限也就越小。不但如此，还可以从有效数字求出其相对误差限。

当用式（1.4.2）表示的近似值具有位有效数字时，显然有

故由式（1.4.2）可知，其相对误差的绝对值

                             （1.4.3）

故相对误差限为

                                   （1.4.4）

式（1.4.4）表达了有效数字与其相对误差限之间的关系。由此可见，有效数字的位数反映了近似值的相对精确度。

上述关系的逆也是成立的，即如果用式（1.4.1）表示的近似值的相对误差能满足

                                （1.4.5）

则至少具有位有效数字（即至少精确到它的第位）。这可证明如下：

由式（1.4.5）及，有

即表示至少具有位有效数字。

例 1  当用3.1416来表示的近似值时，它的相对误差是多少？

解   3.1416具有五位有效数字，，由式（1.4.3）有

例 2  为了使积分的近似值的相对误差不超过，问至少取几位有效数字？

解  可以知道。这样，。由式（1.4.3）有

可解出。即只要取三位有效数字

就能保证的相对误差不大于。