§5 误差的传播与估计

5.1误差估计的一般公式

在实际的数值计算中，参与运算的数据往往都是些近似值，带有误差。这些数据误差在多次运算过程中会进行传播，使计算结果产生误差。而确定计算结果所能达到的精度，显然是十分重要的，但这往往也是件很困难的事。不过，我们对计算误差作出一定的定量估计还是可以做到的。这里介绍一种常用的误差估计的一般公式，它是利用函数的泰勒（Taylor）展开得到的。

先从较简单的二元函数

开始。设和分别是和的近似值，是函数值的近似值，且

函数在点处的泰勒展开式为

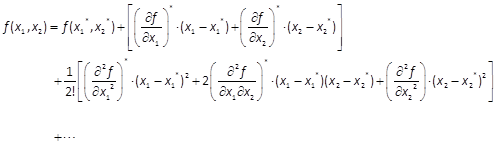
式中，和一般都是小量，如果忽略高阶小量，即高阶的和，则上式可简化为

因此，的绝对误差

                             （1.5.1）

式中，和前面的系数 和分别是和对的绝对误差增长因子，它们分别表示绝对误差和经过传播后增大或减小的倍数。

由式（1.5.1）可得出的相对误差

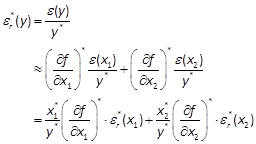        (1.5.2)

式中，和前面的系数和分别是和对的相对误差增长因子，它们分别表示相对误差和经过传播后增大或缩小的倍数。

例3  用电表测得一个电阻两端的电压和流过的电流范围分别为，求这个电阻的阻值R,并估算其绝对误差和相对误差。

解  由欧姆定律，有

可求出R的近似值

由式（1.5.1）可计算的绝对误差

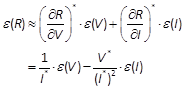
已知把它们代入上式，即可估算出的绝对误差

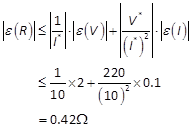
因此，的相对误差

式（1.5.1）和（1.5.2）可推广到更为一般的多元函数

中。只要将函数 在点 处作泰勒展开，并略去其中的等小量的高阶项，即可得到函数的近似值的绝对误差和相对误差的估算式，其分别为

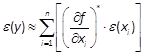                         （1.5.3）

和

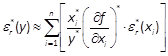                       （1.5.4）

上两式中的各项

和        

分别为各个对的绝对误差和相对误差的增长因子。

从式（1.5.3）和式（1.5.4）可知，当误差增长因子的绝对值很大时，数据误差在运算中传播后，可能会造成结果的很大误差。凡原始数据的微小变化可能引起结果的很大变化的这类问题，称为病态问题或坏条件问题。

5.2 误差在算术运算中的传播

可以利用式（1.5.3）和（1.5.4）对加、减、乘、除、乘方和开方等算术运算中数据误差的传播规律作一具体分析。

1. 加、减运算

由式（1.5.3）及式（1.5.4）有

                             （1.5.5）

及

                         （1.5.6）

由式（1.5.5）可知，近似值之和的绝对误差等于各近似值的绝对误差的代数和。

两数和相减时，由式（1.5.6）有

即

当，即大小接近的两个同号近似值相减时，由上式可知，这时可能会很大，说明计算结果的有效数字将严重丢失，计算精度很低。因此在实际计算中，应尽量设法避开相近数的相减。当实在无法避免时，可用变换计算公式的办法来解决。例如，当要求计算，结果精确到第五位数字时，至少取到

和           

这样

才能达到具有五位有效数字的要求。如果变换算式：

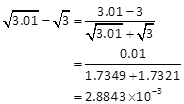
也能达到结果具有五位有效数字的要求，而这时和所需的有效位数只要五位，远比直接相减所需有效位数（八位）为少。

再例如，当很小时， ，如要求得的值，可利用三角恒等式

进行公式变换后再来计算。同理，也可把展开成泰勒级数后，按

 

来进行计算。这两种算法都避开了两个近数相减的不利情况。

2.  乘法运算

由式（1.5.3）及式（1.5.4）有

                       （1.5.7）

和

                          （1.5.8）

由式（1.5.8）可知，近似值之积的相对误差等于相乘各因子的相对误差的代数和。

又由式（1.5.7）可知，当乘数的绝对值很大时，乘积的绝对误差可能会很大，因此也应设法避免。

   3．除法运算

由式（1.5.3）及式（1.5.4）有

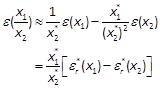                       （1.5.9）

和

由式（1.5.10）可知，两近似值之商的相对误差等于被除数的相对误差与除数的相对误差之差。

  又由式（1.5.9）可知，当除数的绝对值很小、接近于零时，商的绝对误差可能会很大，甚至造成计算机的“溢出”错误，故应设法避免让绝对值太小的数作为除数。

4.乘方及开方运算

由式（1.5.3）及式（1.5.4）有

                           （1.5.11）

及

                              （1.5.12）

由式(1.5.12)可知，乘方运算将使结果的相对误差增大为原值(x)的p（乘方的方次数）倍，降低了精度；开方运算则使结果的相对误差缩小为原值的（为开方的方次数），精度得到了提高。

综上分析可知，大小相近的同号数相减、乘数的绝对值很大以及除数接近于零等，在数值计算中都应设法避免。

5.3 对1算例的误差分析

应用上述误差估计的公式，可对§1中提出的算例中的各种算式作出误差估计和分析，从而可以比较出它们的优劣来。现将结果列于表1-2中。

表1-2

由表1-2可见，从相对误差来看，前两种算法比后两种大许多。原因是及都是相近数相减，这使计算结果的有效数字位数显著减少，第二种算式尤其严重。而后两种算法中，则有效数字的损失较少。由于近似值的次乘方的相对误差是该近似值本身的相对误差的倍，因此，在后两种算法中以最后一种为最佳，这是因为它的乘幂小，是1，故其相对误差最小。可见所选用的算法不同时其计算结果的精度有时会相差至巨。在这个算例中，最好的算式（第四种）的相对误差只有，而最差的算式（第二种）却高达，两者相差约达200倍之巨。由此可见，算法对数值计算的重要程度了。