内容导入:
利用线性代数的知识:任何一个不高于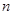 次的多项式,都可以表示成函数
次的多项式,都可以表示成函数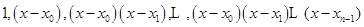 的线性组合,构造牛顿插值多项式。
的线性组合,构造牛顿插值多项式。
在利用线性代数知识的基础上,引入等距节点的概念,构造出牛顿向前差分插值多项式、向后差分多项式、牛顿基本插值多项式。
内容简介:
本节介绍了向前差分与牛顿向前插值公式、向后差分与牛顿向后插值公式、差商与牛顿基本插值公式。
边学边练 :
练习题1 已知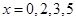 , 对应的函数值为
, 对应的函数值为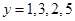 ,用Newton插值多项式求
,用Newton插值多项式求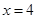 时
时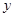 的值。
的值。
练习题2 给定数据表:
构造出函数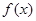 的差商表,并写出它的三次
的差商表,并写出它的三次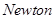 插值多项式。
插值多项式。

练习题1
已知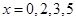 , 对应的函数值为
, 对应的函数值为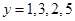 ,用Newton插值多项式求
,用Newton插值多项式求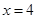 时
时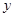 的值。
的值。
解:
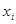
|
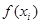
|
一阶差商 |
二阶差商 |
三阶差商 |
0 |
1 |
|
|
|
2 |
3 |
1 |
|
|
3 |
2 |
-1 |
-2/3 |
|
5 |
5 |
3/2 |
5/6 |
3/10 |
所求的三次Newton插值多项式为:
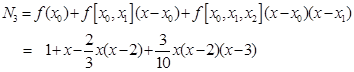
将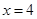 代入上式中,得
代入上式中,得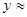 2.07。
2.07。
练习题2
给定数据表:
构造出函数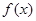 的差商表,并写出它的三次
的差商表,并写出它的三次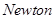 插值多项式。
插值多项式。
解:利用Newton插值公式:
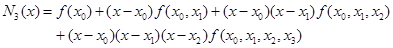
先作出差商表
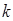
|
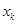
|
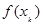
|
一阶差商 |
二阶差商 |
三阶差商 |
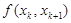
|
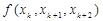
|
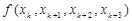
|
0 |
1 |
3 |
|
|
|
1 |
3/2 |
13/4 |
1/2 |
|
|
2 |
0 |
3 |
1/6 |
1/3 |
|
3 |
2 |
5/3 |
-2/3 |
-5/3 |
-2 |
故: