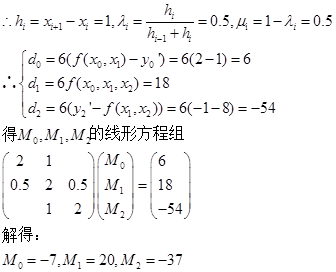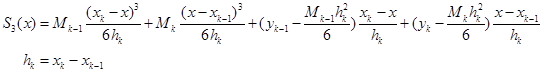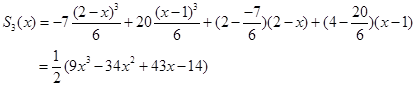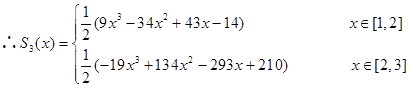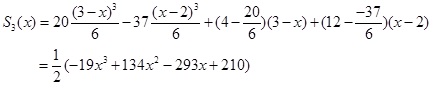内容导入：

分段低次插值虽然具有计算简单、稳定性好、收敛性有保证且易在电子计算机上实现等优点，但它只能保证各小段曲线在连接点上的连续性，却不能保证整条曲线的光滑性（如图2-6中的折线），这就不能满足某些工程技术上的要求。从20世纪60年代开始，首先由于航空、造船等工程设计的需要而发展起来的所谓样条(spline)插值方法，既保留了分段低次插值多项式的各种优点，又提高了插值函数的光滑性。今天，样条插值方法已经成为数值逼近的一个极其重要的分支，在许多领域里得到越来越广泛的应用。

内容简介

本节首先介绍了三次样条插值函数的定义，给出了插值函数满足的三个条件。然后根据插值条件推到插值计算公式。在确定插值公式时出现条件缺少2个，提出在插值区间的边界点处给出，即称为边界条件。并且给出三种常见类型的边界条件：

（1）给定一阶导数值,。

（2）给定二阶导数值,（作为特例，称为自然边界条件。满足自然边界条件的三次样条插值函数称为自然样条插值函数）。

（3）当是周期为的函数时，要求及其导数都是以为周期的函数，相应的边界条件为。

据不同的边界条件推出三次样条插值计算公式。从理论上给出了满足三种边界条件的三次样条插值函数是存在且惟一的定理。

最后给出了相应计算机实现程序的流程图。

边学边练

练习题 根据给定的数据表

	1	2	3
	2	4	12
	1		-1

建立一个三次样条插值函数。