2.1 插值多项式概念及其存在唯一性

2.1.1 插值问题的提法

在生产和科研中出现的函数是多种多样的。常常会遇到这样的情况：在某个实际问题中，虽然可以断定所考虑的函数在区间上存在且连续，但却难以找到它的解析表达式，只能通过实验和观测得到在有限个点上的函数值（即一张函数表）。显然，要利用这张函数表来分析函数的性态，甚至直接求出其他一些点上的函数值可能是非常困难的。在有些情况下，虽然可以写出函数的解析表达式，但由于结构相当复杂，使用起来很不方便。面对这些情况，总希望根据所得函数表（或结构复杂的解析表达式），构造某个简单函数作为的近似。插值法是解决此类问题的一种比较古老的、然而却是目前常用的方法，它不仅直接广泛地应用于生产实际和科学研究中，而且也是进一步学习数值计算方法的基础。

设函数在区间上连续，且在个不同的上分别取值。

插值的目的就是要在一个性质优良、便于计算的函数类中，求一个简单函数，使

            (2.1.1)

而在其他点上，作为的近似值。

通常，称区间为插值区间，称点为插值节点，称式（2.1.1)为插值条件，称函数类Φ为插值函数类，称为函数f（x）在节点处的插值函数。求插值函数的方法称为插值法。

插值函数类Φ的取法不同，所求得的插值函数逼近的效果就不同。它的选择取决于使用上的需要，常用的有代数多项式、三角多项式和有理函数等。当选用代数多项式作为插值函数时，相应的插值问题就称为多项式插值。本章讨论的就是这类插值问题。

在多项式插值中，最常见、最基本的问题是：求一次数不超过的代数多项式

         (2.1.2)

使

          (2.1.3)

其中，为实数；意义同前。

满足插值条件(2.1.3)式的多项式(2.1.2)，称为函数在节点处的次插值多项式。

求函数的次插值多项式的几何意义，就是通过曲线上的个点，作一条次代数曲线，作为曲线的近似，见图2-1。

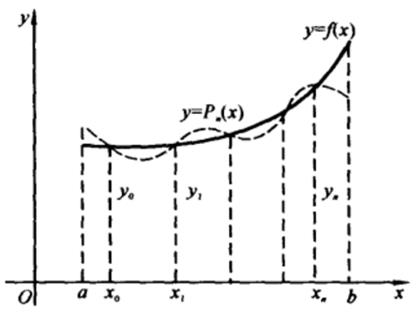
图2-1

2.1.2插值多项式的存在唯一性

由插值条件(2.1.3)式知，插值多项式的系数满足线性方程组

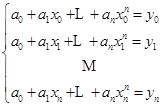          (2.1.4)

由线性代数知，其系数行列式（记为V）是阶范德蒙(Vandermonde)行列式，且

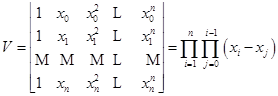
因是区间上不同的点，上式右端乘积中的每一个因子，于是，方程组（2.1.4）的解存在且唯一。故有：

定理1   若节点互不相同，则满足插值条件(2.1.3)式的n次插值多项式(2.1.2)存在且唯一。