2.2 拉格朗日插值多项式

在上一节里，我们不仅指出了插值多项式的存在唯一性，而且也提供了它的一种求法，即通过解线性方程组(2.1.4)来确定其系数。但是，这种做法的计算工作量大，不便于实际应用。在这一节和下一节中，将介绍几种简便的求法。

2.2.1 插值基函数

在求满足插值条件（2.1.3）式的次插值多项式之前，先考虑一个简单的插值问题：对节点中任一点，作一次多项式，使它在该点上取值为1，而在其余点上取值为零，即

                   (2.2.1)

条件(2.2.1)式表明个点都是次多项式的零点，故可设

其中，Ak为待定系数。由条件立即可得

故

      (2.2.2)

对应于每一节点，都能写出一个满足插值条件(2.2.1)式的次插值多项式(2.2.2)。这样，由(2.2.2)式可以写出个次插值多项式。容易看出，这组多项式仅与节点的取法有关，我们称它们为在个节点上的次基本插值多项式或次插值基函数。

2.2.2 拉格朗日插值多项式

利用插值基函数立即可以写出满足插值条件(2.1.3)式的n次插值多项式

              (2.2.3)

事实上，由于每个插值基函数都是次多项式，故其线性组合(2.2.3)式必是不高于次的多项式。同时，根据条件(2.2.1)式容易证多项式(2.2.3)在节点xi处的值为，因此，它就是待求的次插值多项式。

形如式(2.2.3)的插值多项式称为拉格朗日(Lagrange)插值多项式，我们把它记为，即

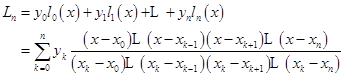   (2.2.4)

作为常用的特例，令n=1，由式(2.2.4)即得两点插值公式

               (2.2.5)

即

               (2.2.6)

这是一个线性函数。用线性函数近似代替函数，在几何上就是通过曲线上的两点和，作一直线近似代替曲线（见图2-2），故两点插值又名线性插值。

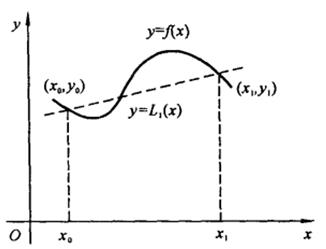
图2-2

若令，由式(2.2.4)又可得到常用的三点插值公式

   (2.2.7)

这是一个二次函数。用二次函数近似代替函数，在几何上就是通过曲线上的三点，和，作一抛物线近似代替曲线（见图2-3），故三点插值又名二次插值或抛物插值。

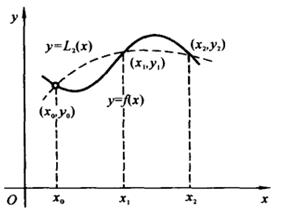
图2-3

已知，，，分别用线性插值和抛物插值求的近似值。

解   因为在之间，故取节点，相应地有。于是由线性插值公式(2.2.5)可得

故用线性插值所求得的近似值为

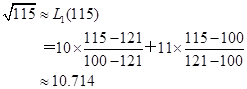
仿上，用抛物插值公式(2.2.7)所求得的近似值为

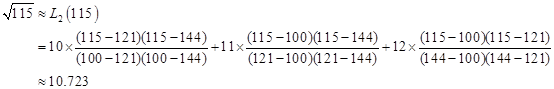
将所得结果与的精确值10.7238…相比较，可以看出抛物插值的精确度较好。

为了便于上机计算，我们常将拉格朗日插值多项式(2.2.4)改写成

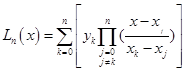               (2.2.8)

公式(2.2.8)的形式对称、结构紧凑。编制程序时（如图2-4），可用二重循环来完成值的计算：先通过内循环，即先固定，令从到累乘求得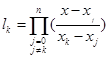，然后再通过外循环，即令从到累加得出插值结果。

在图2-4中给出了利用式(2.2.8)计算处函数值的程序框图。图中的圆圈为循环的终端标志。有些语言规定数组元素的下标值和循环变量的初值必须大于零，此时算式(2.2.8)和框图2-4都需作相应的修改。

 

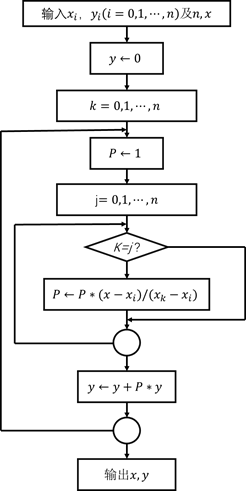
图2-4

2.2.3 插值余项

在插值区间上用插值多项式近似代替，除了在插值节点上没有误差外，在其他点上一般是存在有误差的（见图2-1）。若记

则就是用近似代替时的截断误差。我们称为插值多项式的余项，并且可根据下面的定理来估计它的大小。

定理2  设在区间上有直到阶导数，为上个互异的节点，为满足条件的次插值多项式，那么对于任何，有

                   (2.2.9)

其中，且依赖于。

证明*   由插值条件知，这表明插值节点都是的零点，故可设

                      (2.2.10)

其中，为待定函数。为了求得，对区间上异于的任意一点作辅助函数

不难看出F(t)具有如下特点：

（1）。

（2）在上有直到阶导数，且

              (2.2.11)

由（1）可知在上至少有个互异的零点。根据罗尔(Rolle)定理，在的两个零点之间至少有一个零点，故在(a，b)内至少有个互异的零点。对再应用罗尔定理，推得在内至少有个互异的零点。继续上述讨论，可推得在内至少有一个零点，若记之为，则

于是由(2.2.11)式得

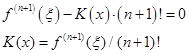
将它代入(2.2.10)式即得(2.2.9)式。

对于，式(2.2.9)显然成立。

例2 在例1中分别用线性插值和抛物插值计算了的近似值，试估计它们的截断误差。

解  用线性插值求的近似值，其截断误差由插值余项公式(2.2.9)知

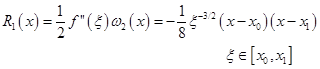
现在,故

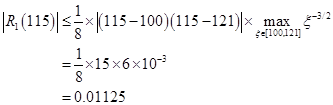
当用抛物插值求的近似值时，其截断误差为

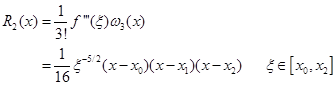
将代入，即得

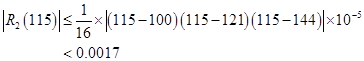
2.2.4  插值误差的事后估计法

在许多情况下，要直接应用余项公式(2.2.9)来估计误差是困难的。下面以线性插值为例，介绍另一种估计误差的方法。

设且已知，若将用和两点作线性插值所求得的近似值记为，用和两点作线性插值所求得的近似值记为，则由余项公式(2.2.9)知

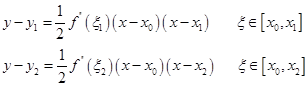
假设在区间内变化不大，将上面两式相除，即得近似式

于是有

即

                 (2.2.12)

近似式(2.2.12)表明，可以通过两个结果的偏差来估计插值误差。这种直接利用计算结果来估计误差的方法，称为事后估计法。

例3 在例1中，曾用和作节点，算得近似值。按同样方法，用和作节点，可算得的另一近似值。由式(2.2.12)可估计出插值结果的误差为