2.3 牛顿插值多项式

由线性代数知，任何一个不高于次的多项式，都可以表示成函数

的线性组合。也就是说，可以把满足插值条件的次插值多项式写成如下形式

其中，为待定系数。这种形式的插值多项式称为牛顿(Newton)插值多项式，我们把它记为，即

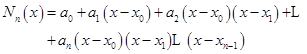               (2.3.1)

因此，牛顿插值多项式是插值多项式的另一种表示形式。与拉格朗日插值多项式相比较，它不仅克服了“增加一个节点时整个计算工作必须重新开始”（见例1）的缺点，而且可以节省乘、除法运算次数。同时，在牛顿插值多项式中用到的差分与差商等概念，又与数值计算的其他方面有着密切的关系。

2.3.1向前差分与牛顿向前插值公式

设函数在等距节点处的函数值为已知，其中是正常数，称为步长。我们称两个相邻点和处函数值之差为函数在点处以为步长的一阶向前差分（简称一阶差分），记作，即

于是，函数f（x）在各节点处的一阶差分依次为

又称一阶差分的差分

为二阶差分。

一般地，定义函数在点处的阶差分为

为了便于计算与应用，通常采用表格形式计算差分，如表2-1所示。

表2-1

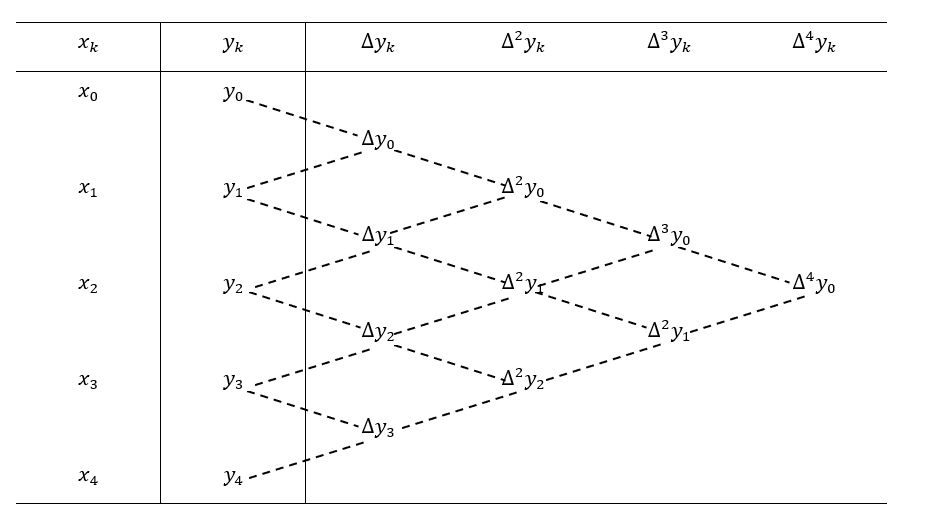
在等距节点情况下，我们可以利用差分表示牛顿插值多项式(2.3.1)的系数，并将所得公式加以简化。事实上，由插值条件立即可得

再由插值条件可得

由插值条件可得

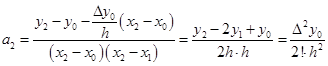
一般地，由插值条件可得

于是，满足插值条件的插值多项式为

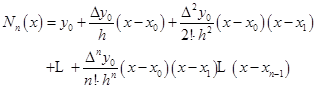
令，并注意到，则可简化为

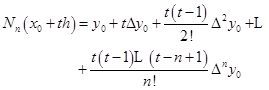                 (2.3.2)

这个用向前差分表示的插值多项式称为牛顿向前插值公式，简称前插公式。它适用于计算表头x0附近的函数值。由插值余项公式(2.2.9)，容易写出前插公式的余项

          (2.3.3)

例4 从给定的正弦函数表（见表2-2左边两列）出发计算，并估计截断误差。

表2-2

解  因为0.12介于0.1与0.2之间，故取，此时。为求,,，…，构造差分表如表2-2所示。表中长方形框中各数依次为在处的函数值和各阶差分。若用线性插值求的近似值，则由前差公式(2.3.2)立即可得

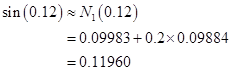
用二次插值得

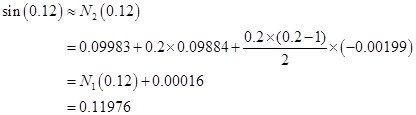
用三次插值得

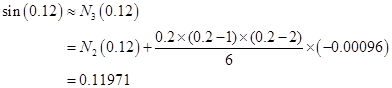
因与很接近，且由差分表2-2可以看出，三阶差分接近于常数（即接近于零），故取作为的近似值，此时由余项公式(2.3.3)可知其截断误差

2.3.2 向后差分与牛顿向后插值公式

在等距节点下，除了上面提到的向前差分外，还可引入向后差分和中心差分，它们的定义和记号分别如下：

在点处以为步长的一阶向后差分和阶向后差分分别为

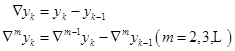
在点处以为步长的一阶中心差分和阶中心差分分别为

  

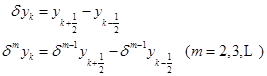
其中，，。

各阶向后差分与中心差分的计算，可通过构造向后差分表与中心差分表来完成（参见表2-2）。

利用向后差分，可以简化牛顿插值多项式(2.3.1)，导出与牛顿向前插值公式(2.3.2)类似的公式。事实上，若将节点的排列次序看作，那么(2.3.1)式可写成

根据插值条件，通过导出式(2.3.2)类似的途径，可得到一个用向后差分表示的插值多项式

      (2.3.4)

其中，t<0。插值多项式(2.3.4)称为牛顿向后插值公式，简称后插公式。它适用于计算表尾附近的函数值。由插值余项公式(2.2.9)，可写出后插公式的余项

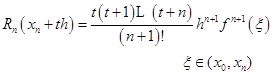                (2.3.5)

例5 已知函数表同例4，计算，并估计截断误差。

解   因为位于表尾附近，故用后插公式(2.3.4)计算的近似值。

按理，为了计算函数在处的各阶向后差分，应构造向后差分表。但由向前差分与向后差分的定义可以看出，对同一函数表来说，构造出来的向后差分表与向前差分表在数据上完全相同。因此，表2-2中用“＿”线标出的各数依次给出了在处的函数值和各阶向后差分值。

因三阶向后差分接近于常数，故用三次插值进行计算，且，于是由后插公式(2.3.4)得

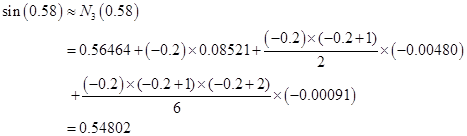
因为在整个计算中，只用到四个点上的函数值，故由余项公式(2.3.5)知其截断误差

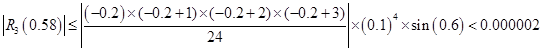
2.3.3 差商与牛顿基本插值多项式

当插值节点非等距分布时，就不能引入差分来简化牛顿插值多项式，此时就要用到差商这个新概念和它的记号。  设函数在一串互异的点上的值依次为。我们称函数值之差与自变量之差的比值

为函数关于点的一阶差商（简称一阶差商），记作。例如

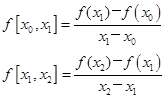
又称一阶差商的差商

为函数关于点的二阶差商（简称二阶差商），记作。例如

一般地，可通过函数的阶差商定义的阶差商如下：

和计算差分类似，在计算差商时常采用表格（称为差商表）的形式，如表2-3所示。

表2-3

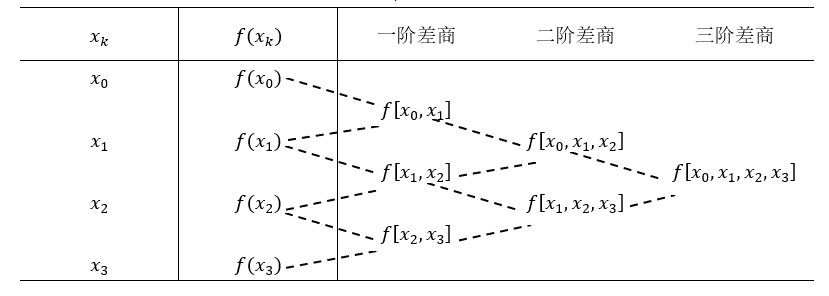
差商具有下列重要性质（证明略）：

（1） 函数的阶差商可由函数值的线性组合表示，且

（2）差商具有对称性，即任意调换节点的次序，不会影响差商的值。例如

（3）当在包含节点的某个区间上存在时，在之间必有一点，使

（4）在等距节点情况下，可同时引入阶差分与差商，且有下面关系：

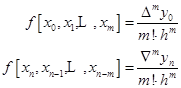
引入差商的概念与记号后，可以利用差商表示牛顿插值多项式(2.3.1)的系数。事实上，从插值条件出发，可以像确定前插公式中的系数那样，逐步地确定式(2.3.1)中的系数

 

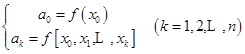
故满足插值条件的次插值多项式为

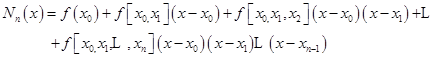     （2.3.6)

这个用差商表示的插值多项式，称为牛顿基本插值多项式，常被用来计算非等距点上的函数值。

例6 试用牛顿基本插值多项式按例1 要求重新计算的近似值。 

解  先构造差商表如表2-4所示。由表可以看出牛顿基本插值多项式(2.3.6)中各系数依次为

表2-4

故用线性插值所求得的近似值为

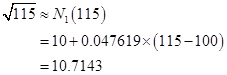
用抛物插值所求得的近似值为

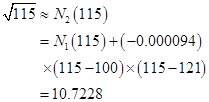
所得结果与例1 相一致。

比较例1和例6的计算过程可以看出，与拉格朗日插值多项式相比较，牛顿插值多项式的优点是明显的。

最后指出，由插值多项式的存在唯一性定理知，满足同一组插值条件的拉格朗日插值多项式(2.2.4)与牛顿基本插值多项式(2.3.6)实际上是同一个多项式，因此，余项公式(2.2.9)也适用于牛顿插值。但是，在实际计算时，有时也用差商表示的余项公式

                 (2.3.7)

来估计截断误差。余项公式(2.3.7)的证明可以在许多数值分析书中找到，此处从略。但需要说明的是，式中的阶差商与的值（它正是我们要计算的）有关，故不可能准确的计算出的精确值，只能对它作出一种估计。例如，当四阶差商变化不大时，可用近似代替。