2.4 分段低次插值

例2和例4表明，适当地提高插值多项式的次数，有可能提高计算结果的准确程度。但是决不可由此得出结论，认为插值多项式的次数越高越好。

例如，我们对函数

先以为节点作次插值多项式，再以为节点作10次插值多项式，并将曲线， 及，描绘在同一坐标系中，如图2-5所示。

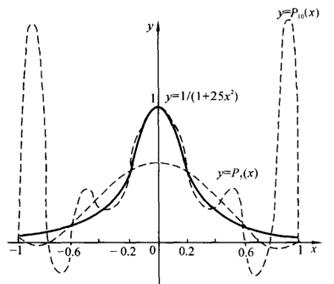
图2-5

由图2-5可以看出，虽然在局部范围内，例如在区间中，比较好地逼近，但从整体来看，并非处处都比更好地逼近，尤其是在区间的端点附近。进一步的分析表明，当增大时，该函数在等距节点下的高次插值多项式在两端会发生激烈的振荡。这种现象（称为龙格(Runge)现象）表明，在大范围内使用高次插值，逼近的效果可能是不理想的。

另一方面，插值误差除来自截断误差外，还来自初始数据的误差和计算过程中的舍入误差。插值次数越高，计算工作量越大，积累误差也可能越大。

因此，我们很少采用高次插值。在实际计算中，常常用分段低次插值进行计算，即把整个插值区间分成若干个小区间，在每个小区间上进行低次插值。

例如，当给定了个点上的函数值后，若要计算点处函数值的近似值。可先选取两个节点与 ，使，然后在小区间上作线性插值，即得

                           (2.4.1)

这种分段低次插值叫分段线性插值。在几何上就是用折线代替曲线，如图2-6所示。故分段线性插值又称折线插值。

类似地，为求的近似值，也可选取距点最近的三个节点进行二次插值，即取

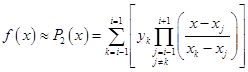                               (2.4.2)

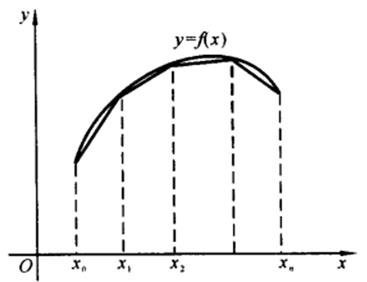
图2-6

这种分段低次插值叫分段二次插值。在几何上就是用分段抛物代替曲线，故分段二次插值又称分段抛物插值。为了保证是距点较近的三个节点，式(2.4.2)中的可以通过下面方法确定：

  

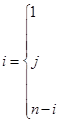
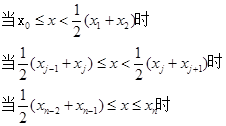
相应的程序框图见图2-7。

 

 

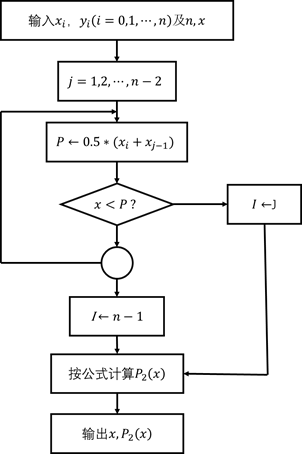
图2-7