2.5 三次样条插值

分段低次插值虽然具有计算简单、稳定性好、收敛性有保证且易在电子计算机上实现等优点，但它只能保证各小段曲线在连接点上的连续性，却不能保证整条曲线的光滑性（如图2-6中的折线），这就不能满足某些工程技术上的要求。从20世纪60年代开始，首先由于航空、造船等工程设计的需要而发展起来的所谓样条(spline)插值方法，既保留了分段低次插值多项式的各种优点，又提高了插值函数的光滑性。今天，样条插值方法已经成为数值逼近的一个极其重要的分支，在许多领域里得到越来越广泛的应用。

本书介绍应用最广且具有二阶连续导数的三次样条插值函数。

2.5.1 三次样条插值函数的定义

对于给定的函数表

若函数满足：

（1）在每个子区间上是不高于三次的多项式。

（2），，在上连续。

（3）满足插值条件，则称为函数关于节点的三次样条插值函数。

2.5.2 边界条件问题的提出与类型

必须指出，单靠一张函数表是不能完全确定一个三次样条插值函数的。

事实上，由条件（1）知，三次样条插值函数是一个分段三次多项式，若用表示它在第个子区间上的表达式，则形如

这里有四个待定系数。子区间共有个，要确定需要确定个待定系数。

另一方面，要求分段三次多项式及其导数和在整个插值区间 上连续，只要它们在各子区间的连接点上连续即可。故由条件（2）和条件（3）可得待定系数应满足的个方程

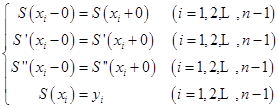               (2.5.1)

由此可以看出，要确定个待定系数还缺少两个条件。这两个条件通常在插值区间的边界点处给出，称为边界条件。

边界条件的类型很多，常见的有：

（1）给定一阶导数值,。

（2）给定二阶导数值,（作为特例，称为自然边界条件。满足自然边界条件的三次样条插值函数称为自然样条插值函数）。

（3）当是周期为的函数时，要求及其导数都是以为周期的函数，相应的边界条件为

（由的周期性知，从而必有，故不必再提出此要求）。

2.5.3 三次样条插值函数的求法

虽然可以利用方程组(2.5.1)和边界条件求出所有待定系数，从而得到三次样条插值函数在各子区间的表达式，但是，这种做法的计算工作量大，不便于实际应用。下面介绍一种简便的求法。

设在节点处的二阶导数为

因为在子区间上是不高于三次的多项式，其二阶导数必是线性函数（或常数）。于是，有

记，则有

连续积分两次得

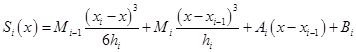          (2.5.2)

其中，和为积分常数。利用插值条件

易得

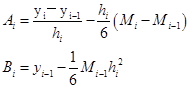
将它们代入式(2.5.2)，加以整理后即得

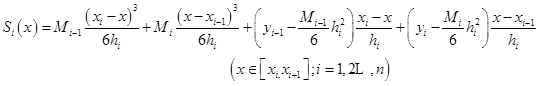 (2.5.3)

综合以上讨论可知，只要确定这个值，就可以定出三次样条插值函数。

为了求出，我们利用一阶导数在子区间连接点上连续的条件

即

                         (2.5.4)

由式(2.5.3)可得

       (2.5.5)

故

                    (2.5.6)

将式(2.5.5)中的改为，即得在子区间上的表达式，并由此得

                  (2.5.7)

将式(2.5.6)和式(2.5.7)代入式(2.5.4)，整理后得

上式两边同乘以，即得方程

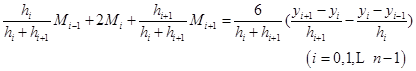
若记

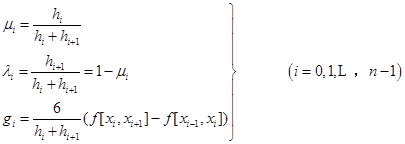        (2.5.8)

   

则所得方程可简写成

即

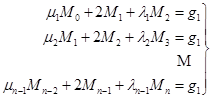                       (2.5.9)

这是一个含有个未知数、个方程的线性方程组。要确定的值，还需用到边界条件。

在第（1）种边界条件下，由于和已知，我们可以得到包含有的两个线性方程。实际上，由式(2.5.5)知，在子区间上的导数为

故由条件立即可得

即

                        (2.5.10)

同理，由条件可得

                      (2.5.11)

将式(2.5.9)和式(2.5.10)以及式(2.5.11)合在一起，即得确定的线性方程组

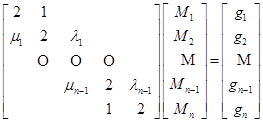                   （2.5.13）

其中

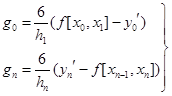                         (2.5.13)

在第（2）种边界条件下，由于和已知，在方程组(2.5.9)中实际上只包含有个未知数，并且可以改写成

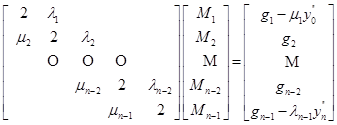              (2.5.14)

在第（3）种边界条件下，由直接可得

                                 (2.5.15)

由条件可得

注意到和，将上式整理后得方程

若记

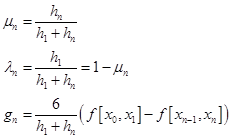
则所得方程可简写成

                     (2.5.16)

将式(2.5.9)，(2.5.15)，(2.5.16)合在一起，即得确定的线性方程组

              (2.5.17)

利用线性代数知识，可以证明方程组(2.5.12)，(2.5.14)及(2.5.17)的系数矩阵都是非奇异的，从而都有唯一确定的解。

针对不同的边界条件，解相应的方程组(2.5.12)或(2.5.14)或(2.5.17)，求出的值，将它们代入式(2.5.3)，就可以得到在各子区间上的表达式。

综合以上分析，有

定理3  对于给定的函数表

满足第（1）或第（2）或第（3）种边界条件的三次样条插值函数是存在且惟一的。

三次样条插值函数的具体求解过程，在下面例子中给出了详细说明。

例7   已知函数的函数值如下：

 

在区间，上求三次样条插值函数，使它满足边界条件。

解  先根据给定数据和边界条件算出，与，写出确定的线性方程组。在本例中，给出的是第（1）种边界条件，确定的线性方程组形如式(2.5.12)。由所给函数表知

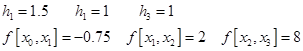
于是，由，与的算式(2.5.8)知

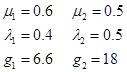
由第（1）边界条件下g0与gn的计算公式(2.5.13)知

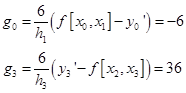
故确定与的方程组为

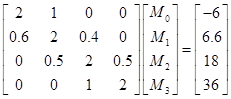               ①

然后解所得方程组，得到在各节点上的值。在本例中，解 式得

最后将所得代入式，即得在各子区间上的表达式。由式(2.5.3)知，在上的表达式为

                                         

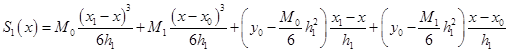
在本例中，将,, ,,,,代入，整理后得

同理可得

故所求三次样条插值函数为

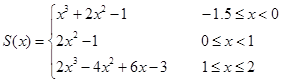
在第（1）种边界条件下，计算三次样条插值函数在点处函数值的程序框图，如图2-8所示。在第六章中介绍的许多方法，都可用来求解方程组(2.5.12)，但是，由于其系数矩阵是严格对角占优势（即主对角线上的元素的绝对值都严格地大于同一行其余元素的绝对值之和）的三对角线型矩阵，故用第六章中介绍的追赶法求解更佳。

图2-8

上述求三次样条插值函数的方法，其基本思路和特点是：先利用一阶导数在内节点上的连续性以及边界条件，列出确定二阶导数的线性方程组（在力学上称为三弯矩方程组），并由此解出，然后用来表达。

实际上，还可以通过别的途径来求取三次样条插值函数。例如，可以先利用二阶导数在内节点上的连续性以及边界条件，列出确定一阶导数的线性方程组（在力学上称为三转角方程组），并由此解出，然后用来表达。在有些情况下，这种表达方法与前者相比较，使用起来更方便。

用三次样条插值函数逼近被插值函数的效果，可参考下节的例8。