当前位置:课程学习>>第二章>>知识讲解>>你问我答
1.简述插值法方法的概念。
2.求一个次数不高于3的多项式![]() 使之满足插值条件:
使之满足插值条件:
![]()
3. 通过点![]() ,
, ![]() ,
, ![]() 所作的插值多项式是( )
所作的插值多项式是( )
(A) 二次的 (B) 一次的 (C) 不超过二次的 (D) 大于二次的
4. 函数![]() 在节点
在节点![]() 处的二阶差商
处的二阶差商![]()
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
5. 通过四个互异节点的插值多项式P(x),只要满足( ), 则P(x)是不超过一次多项式。
(A)初始值y0=0 (B) 所有一阶差商为0
(C) 所有二阶差商为0 (D) 所有三阶差商为0
6. 拉格朗日插值多项式的余项是( ),牛顿插值多项式的余项是( )
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
7.掌握差分的概念以及列出差分表的方法,掌握牛顿向前插值多项式和牛顿向后插值多项式的表达形式及相应插值余项的形式。


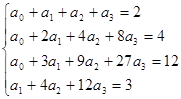 ,解得:
,解得: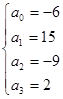 ,
, 