3.3 最小二乘解的求法

由最小二乘解(式(3.2.4))应满足的条件(3.2.5)式知，点是多元函数

的极小点，从而满足方程组

即

亦即

若对于任意函数和，引入记号

                                (3.3.1)

则上述方程组可以表示成

           

写成矩阵形式即

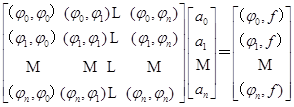                     (3.3.2)

方程组(3.3.2)称为法方程组。当线性无关时，可以证明它存在有惟一解

并且相应的函数式(3.2.4)就是满足条件(3.2.5)式的最小的二乘解。

综上分析可得：

定理1   对于给定的一组实验数据,(互异;)在函数类

(且线性无关)中，存在惟一的函数

使得关系式(3.2.5)成立，并且其系数可以通过解法方程组(3.3.2)得到。

作为曲线拟合的一种常用的情况，若讨论的是代数多项式拟合，即取

则由式(3.3.1)知

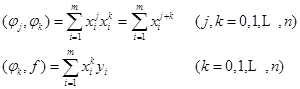
故相应的法方程组为

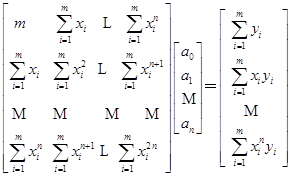                  (3.3.3)

下面，我们通过两个具体例子来说明用最小二乘法解决实际问题的具体步骤与某些技巧。

例 1  某种铝合金的含铝量为，其熔解温度为,由实验测得与的数据如表3-1左边三列。试用最小二乘法建立与之间的经验公式。

解   根据前面讨论，解决问题的过程如下：

将表中给出的数据点描绘在坐标纸上，如图3-1所示。

表  3-1

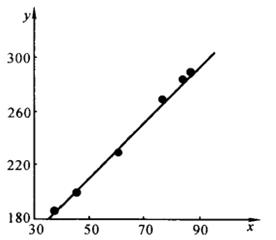
图 3-1

(2)确定拟合曲线的形式。由图3-1可以看出，六个点位于一条直线的附近，故可以先用线性函数(直线)来拟合这组实验数据，即令

                                    ①

其中，为待定常数。

(3)建立法方程组。由于问题归结为一次多项式拟合问题，故由①式知，相应的法方程组形如

 

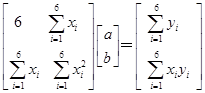
经过计算(见表3-1)，即得确定待定数的法方程组

                           ②

(4)解方程组②得

将所得的结果带入①式得经验公式

                               ③

所得经验公式能否较好地反映客观规律，还需通过实践来检验。由③式算出的函数值(称为拟合值)

与实测值之间有一定偏差。

表 3-2

	1	2	3	4	5	6
	36.9	46.7	63.7	77.8	84.0	87.5
	177.78	199.67	237.64	269.13	282.98	290.80
	181	197	235	270	283	292
	-3.22	2.67	2.64	-0.87	-0.02	-1.20
	10.37	7.13	6.97	0.76	0.0004	1.44
	26.6704

由表3-2可以看出，偏差的平方和=26.6704，其平方根 (称为均方误差)在一定程度上反映了所得经验公式的好坏。同时，由表3-2还可以看出，最大偏差。如果认为这样的误差都允许的话，我们就可以用经验公式③来计算含铝量在之间的熔解温度。否则，就要用改变函数类型或者增加实验数据等办法来建立新的经验公式。

例 2  在某化学反应里，测得生成物浓度与时间的数据见表3-3，试用最小二乘法建立与之间经验公式

表  3-3

解   将已知数据点描绘在坐标纸上，见图3-2。由图3-2及问题的物理背景可以看出，拟合曲线 应具有下列特点：

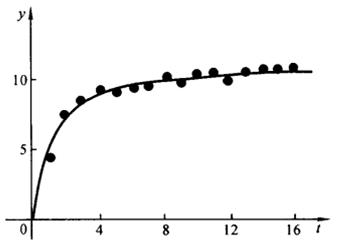
图   3-2

曲线随着t的增加而上升，但上升速度由快到慢。

当，反应尚未开始，即时，趋于某一常数。故曲线应通过原点（或者当时以原点为极限点），且有一水平渐进线。

具有上述特点的曲线很多。选用不同的数学模型，可以获得不同的拟合曲线与经验公式。

下面提供两种方案。

方案1  设想是双曲线型的，并且具有下面的形式

                            ①

此时，若直接按最小二乘原则去确定参数和，则问题归结为求二元函数

                     ②

的极小点，这将导致求解非线性方程组

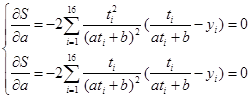
给计算带来了麻烦。在这里，我们通过变量替换将它转化为关于待定参数的线性函数。为此，将①式改写成

于是，若引入新变量

则①式就是

同时，由题中所给数据表3-3可以算出新的数据表（为节约篇幅，在表中3-4中仅列出部分数据）。这样，问题就归结为：根据数据表3-4，求形如的最小二乘解。

表3-4

参照例1的做法，解法方程组

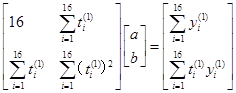
既得

代入①式，得经验公式

                      ③

方案2 设想具有指数形式 

                       ④

为了在求取参数和时，避免求解一个非线性方程组，对上式两边取对

此时若引入新变量

表3-5

并记，则上式就是

又由数据表3-3颗算出新的数据表3-5。于是将问题归结为：根据数据表3-5，求形如的最小二乘解。参照方案1，写出相应的法方程组并解之，即得

于是

故得另一个经验公式

                          ⑤

我们把两个不同的经验公式③和⑤进行了比较（见表3-6），从均方误差与最大偏差这两个不同的角度看，后者均优于前者。因此，在解决实际问题时，常常要经过反复分析，多次选择、计算与比较，才能获得较好的数学模型。

表3-6

经验公式	均方误差	最大偏差
③式
⑤式

最后，我们以常用的多项式拟合为例，说明最小二乘法在电子计算机上实现的步骤。

设有一组实验数据，今要用最小二乘法求一个次多项式曲线

来拟合这组数据。

显然，求的实质就是要确定其系数。由前面讨论知，问题可归结为建立和求解法方程组（3.3.3）。

图3-3

为了便于编制程序并减少计算工作量，引入矩阵

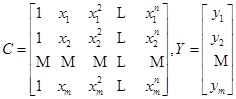
则法方程组（3.3.3）的系数矩阵（用表示）和右端向量（用表示）分别为

相应的程序框图如图3-3所示，其中中间矩阵的生成方法见框图3-4。

图3-4