3.4 加权最小二乘数

在实际问题中测得的所有实验数据，并不总是等精度、等地位的。显然，对于精度较高或地位较重要（这应根据具体情况来判定）的那些数据，应给予较大的权。在这种情况下，求给定数据的拟合曲线，就要采用加权最小二乘法。

用加权最小二乘法进行曲线拟合的要求与原则是：对于给定的一组实验数据要求在某个函数类中，寻求一个函数

使

其中，为函数类中任一函数； 是一列正数，称为权，它的大小反映了数据地位的强弱。

显然，求的问题可归结为求多元函数

的极小点。采用本章§3类似的方法，仍可得法方程组（3.3.2），但其中

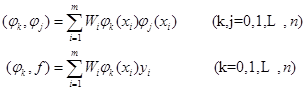
作为特例，如果选用的拟合曲线为

那么，相应的法方程组为

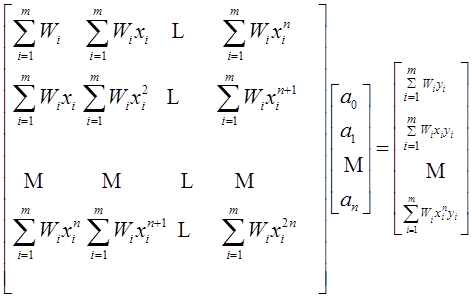 （3.4.1）

例3 已知一组实验数据 及权如表3-7所示。若与之间有线性关系，试用最小二乘法确定系数和。

表3-7

解  因为拟合曲线为一次多项式曲线（直线），故相应的法方程组形如式（3.4.1）。将表中各已知数据代入即得法方程组

解之得