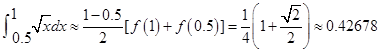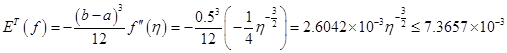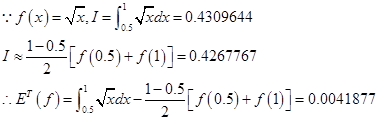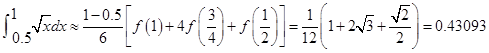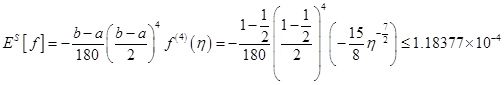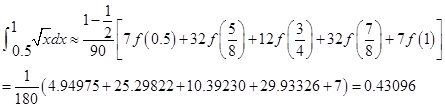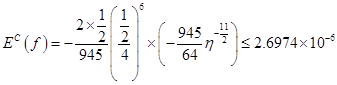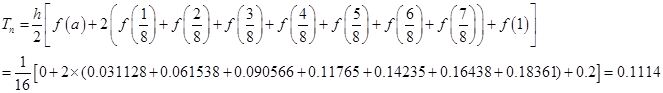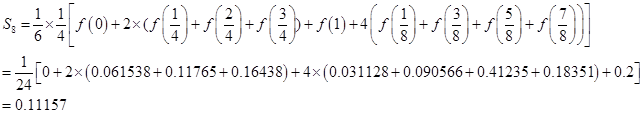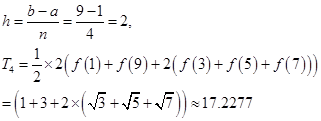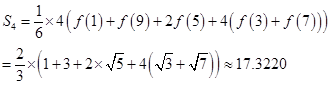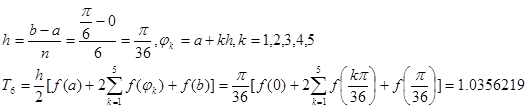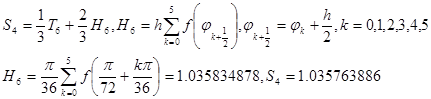内容导入：

在插值型求积公式及其构造方法上，考虑到计算上的方便，常将积分区间等分之，并取分点为求积节点，构造出来的插值型求积公式就称为牛顿—柯特斯公式。

内容简介

由插值型求积公式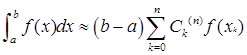出发，推出梯形公司、辛普生公式、柯斯特公式。

为了既能提高结果的精度，又使算法简便且易在电子计算机上实现，先将积分区间分成几个小区间，并在每个小区间上用低阶牛顿—柯特斯公式计算积分的近似值，然后对这些近似值求和，从而得到所求积分的近似值。得到复合求积公式。并且讨论其收敛性，给出了余项定理和p阶收敛的概念。

讨论误差的事后估计，给出了步长的自动选择。最后得到了复合梯形法的递推公式。

边学边练

练习题1 分别用梯形公式、Simpson公式、Cotes公式计算积分计误差。

练习题2 分别用复合梯形公式和复化公式Simpson计算下列积分.

(1)，（2），（3）