4.1 数值积分导引

4.1.1讨论数值求积的必要性

在高等数学中，曾用牛顿—莱布尼茨（Newton-Leibniz）公式

（其中，是的一个原函数）来计算定积分。但是，在工程技术和科学研究中，常常遇到如下情况：

(1)的结构复杂，求原函数困难。

(2)的原函数不能用初等函数表示。

(3)的精确表达式不知道，只给出了一张由实验提供的函数表。

对于这些情况，要计算积分的准确值都是十分困难的，这就要求建立积分的近似计算方法。此外，积分的近似算法又为其他一些数值方法，例如微分方程数值解、积分方程数值解等，提供了必要的基础。

4.1.2构造数值求积公式的基本方法

我们可以从不同的角度出发通过各种途径来构造数值求积公式。但常用的一个方法是，利用插值多项式来构造数值求积公式。具体做法如下：

在积分区间上取一组点

作的次插值多项式

其中,为次插值基函数。用近似代替被积函数，则得

                      （4.1.1）

若记

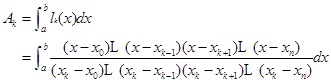               （4.1.2）

则得数值求积公式

                           （4.1.3）

形如式（4.1.3）的求积公式称为机械求积公式，其中称为求积节点，称为求积系数。若求积公式（4.1.3）中的求积系数是由式（4.1.2）确定的，则称该求积公式为插值型求积公式。

本章主要讨论插值型求积公式。

4.1.3  求积公式的余项

积分的真值与由某求积公式给出的近似值之差，称为该求积公式的余项，记作。例如，求积公式（4.1.3）的余项为

如果求积公式（4.1.3）是插值型，则由上式可知

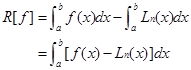
于是，由插值余项公式得

  　　　　　                  （4.1.4）

其中，。

4.1.4求积公式的代数精度

为了使一个求积公式能对更多的积分具有较好的实际计算意义，就应该要求它对尽可能多的被积函数都准确地成立。在计算方法中，常用代数精度这个概念来描述它。

定义1  若求积公式

对任意不高于次的代数多项式都准确地成立，而对于却不能准确地成立，则称该求积公式的代数精度为。

例如，读者熟知的梯形公式（在几何上，就是用梯形面积近似代替曲边梯形面积，见图4-1）

  　　　　　　　　　　　  　　　　　　　   （4.1.5）

的代数精度。

事实上，当时，在式（4.1.5）中：

左端=

右端=

左端=右端

这表明求积公式（4.1.5）对是准确成立的。

当时，在式（4.1.5）中：

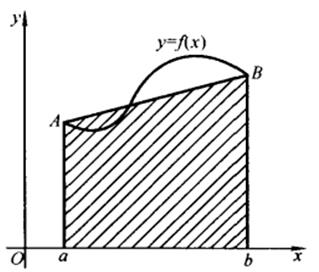
图 4-1

左端=

右端=

左端=右端    

这表明求积公式（4.1.5）对也是准确成立的。

综上所述，容易看出求积公式（4.1.5）对函数和的任一线性组合——不高于一次的代数多项式都准确成立，故公式（4.1.5）的代数精度至少等于1。但是，当时，即有

左端=

右端=

左端≠右端   (设)

故由定义知，梯形公式（4.1.5）的代数精度。

显然，一个求积公式的代数精度越高，它就越能对更多的被积函数准确（或较准确）地成立，从而具有更好的实际计算意义。

由插值型求积公式的余项式（4.1.4）易得：

定理1  含有个节点的插值型求积公式（4.1.3）的代数精度至少为。