知识点二:牛顿——柯特斯公式
4.2 牛顿——柯特斯公式
在第1节中,我们介绍了插值型求积公式及其构造方法。在实际应用时,考虑到计算上的方便,常将积分区间等分之,并取分点为求积节点。这样构造出来的插值型求积公式就称为牛顿——柯特斯(Newton-Cotes)公式。
本节在介绍一般牛顿-柯特斯公式的基础上,介绍几个常用的牛顿——柯特斯公式以及这些公式在实际计算时的用法。
4.2.1 牛顿——柯特斯公式
若将积分区间![]() 等分,取分点
等分,取分点
![]()
作为求积节点,并作变量替换![]() ,那么插值型求积公式(4.1.3)的系数由式(4.1.2)可得
,那么插值型求积公式(4.1.3)的系数由式(4.1.2)可得
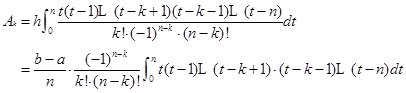
记
![]() (4.2.1)
(4.2.1)
则
![]()
于是,由式(4.1.3)就可以写出相应的插值型求积公式
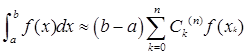 (4.2.2)
(4.2.2)
这就是一般的牛顿—柯特斯公式,其中![]() 称为柯特斯系数。
称为柯特斯系数。
从柯特斯系数的算式(4.2.1)可以看出,其值与积分区间![]() 及被积函数
及被积函数![]() 都无关,只要给出了积分区间的等分数
都无关,只要给出了积分区间的等分数![]() ,就能按式(4.2.1)毫无困难地算出
,就能按式(4.2.1)毫无困难地算出![]() 。例如,当
。例如,当![]() 时有
时有
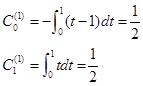
当![]() 时有
时有
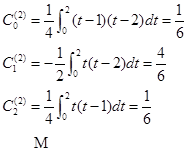
为了便于运用,我们将部分柯特斯系数列在表4-1中。
利用这张柯特斯系数表,由(4.2.2)可以直接写出当![]() 时的牛顿—柯特斯公式。例如,当
时的牛顿—柯特斯公式。例如,当![]() 时有两点公式
时有两点公式
![]() (4.2.3)
(4.2.3)
当![]() 时有三点公式
时有三点公式
![]() (4.2.4)
(4.2.4)
表4-1
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
当![]() 时有五点公式
时有五点公式
![]() (4.2.5)
(4.2.5)
其中,![]() 。
。
求积公式(4.2.3)就是梯形公式。
求积公式(4.2.4)称为辛普生(Simposn)公式。其几何意义就是用通过A,B,C三点的抛物线![]() 围成的曲边梯形面积近似地代替原曲边梯形面积(见图4-2)。因此,求积公式(4.2.4)又名抛物线公式。
围成的曲边梯形面积近似地代替原曲边梯形面积(见图4-2)。因此,求积公式(4.2.4)又名抛物线公式。
求积公式(4.2.5)称为柯特斯公式。
梯形公式、辛普生公式和柯特斯公式,是三个最基本、最常用的等距节点下的求积公式。下述定理给出了这些求积公式的余项:
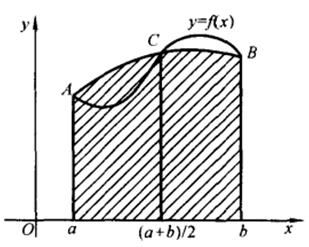
图 4-2
定理2 若![]() 在
在![]() 上连续,则梯形公式(4.2.3)的余项为
上连续,则梯形公式(4.2.3)的余项为
![]() (4.2.6)
(4.2.6)
若![]() 在
在![]() 上连续,则辛普生公式(4.2.4)的余项为
上连续,则辛普生公式(4.2.4)的余项为
![]() (4.2.7)
(4.2.7)
若![]() 在
在![]() 上连续,则柯特斯公式(4.2.5)的余项为
上连续,则柯特斯公式(4.2.5)的余项为
![]() (4.2.8)
(4.2.8)
其中,![]() 。
。
定理2的证明从省略。
4.2.2 复合牛顿——柯特斯公式
容易看出,当积分区间![]() 较大时,直接使用牛顿——柯特斯公式所得积分近似值的精度是很难得到保证的。因此,在实际应用中,为了既能提高结果的精度,又使算法简便且易在电子计算机上实现,往往采用复合求积的方法。
较大时,直接使用牛顿——柯特斯公式所得积分近似值的精度是很难得到保证的。因此,在实际应用中,为了既能提高结果的精度,又使算法简便且易在电子计算机上实现,往往采用复合求积的方法。
所谓复合求积,就是先将积分区间分成几个小区间,并在每个小区间上用低阶牛顿—柯特斯公式计算积分的近似值,然后对这些近似值求和,从而得到所求积分的近似值。由此得到的一些具有更大实用价值的数值求积公式,统称为复合求积公式。
例如,先将区间![]()
![]() 等分,记分点为
等分,记分点为
![]()
其中,![]() 称为步长。然后在每个小区间
称为步长。然后在每个小区间![]() 上应用梯形公式(4.2.3),即
上应用梯形公式(4.2.3),即
![]()
就可导出复合梯形公式
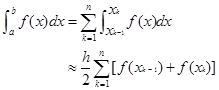
若将所得积分近似值记为![]() ,并注意到
,并注意到![]() ,则上式即
,则上式即
![]() (4.2.9)
(4.2.9)
仿上,可得复合辛普生公式
![]() (4.2.10)
(4.2.10)
和复合柯特斯公式
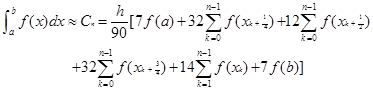 (4.2.11)
(4.2.11)
在式(4.2.10)和式(4.2.11)中:
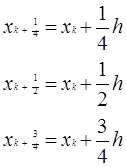
定理3 若![]() 在积分区间
在积分区间![]() 上分别具有二阶、四阶和六阶连续导数,则复合求积公式(4.2.9)、(4.2.10)、(4.2.11)的余项分别为
上分别具有二阶、四阶和六阶连续导数,则复合求积公式(4.2.9)、(4.2.10)、(4.2.11)的余项分别为
![]() (4.2.12)
(4.2.12)
![]() (4.2.13)
(4.2.13)
![]() (4.2.14)
(4.2.14)
其中,![]() ,且当
,且当![]() 充分小时,又有
充分小时,又有
![]() (4.2.15)
(4.2.15)
![]() (4.2.16)
(4.2.16)
![]() (4.2.17)
(4.2.17)
证明 我们只对复合梯形公式(4.2.9)证明余项公式(4.2.12)和(4.2.15),其余留给读者自己完成。
先证式(4.2.12)。由于![]() 在
在![]() 上连续,故由定理2知,对每个小区间上积分
上连续,故由定理2知,对每个小区间上积分![]() 使用梯形公式时,所得近似值的误差为
使用梯形公式时,所得近似值的误差为![]() ,故
,故
![]() (4.2.18)
(4.2.18)
即
![]()
因为
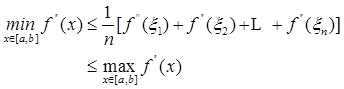
由中值定理知,在![]() 中必有点
中必有点![]() ,使
,使
![]()
故余项公式(4.2.12)成立。
再证式(4.2.15)。由式(4.2.18)和定积分的定义,有
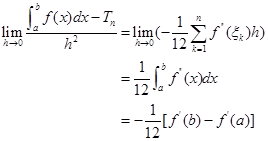 (4.2.19)
(4.2.19)
故当![]() 充分小时,式(4.2.15)成立。
充分小时,式(4.2.15)成立。
由余项公式(4.2.12)~(4.2.17)可以看出,只要所涉及的各阶导数在积分区间![]() 上连续,则当
上连续,则当![]() (即
(即![]() )时,
)时,![]() ,
,![]() 和
和![]() 都收敛于积分真值
都收敛于积分真值![]() ,而且收敛速度一个比一个快。
,而且收敛速度一个比一个快。
定义2 对于复合求积公式![]() ,若当
,若当![]() 时有
时有
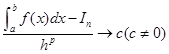
则称![]() 是p阶收敛的。
是p阶收敛的。
定理4 复合求积公式(4.2.9)、(4.2.10)和(4.2.11)分别具有二阶、四阶和六阶收敛性。
证明 根据收敛的定义,由式(4.2.19)立即可以看出,复合梯形公式(4.2.9)具有二阶收敛性。
按同样的思路,可以证明复合辛普生公式(4.2.10)和复合柯特斯公式(4.2.11)分别具有四阶和六阶收敛性。具体证明过程也留给读者自己完成。
对于一个数值求积公式来说,收敛阶越高,近似值![]() 收敛到真值
收敛到真值![]() 的速度就越快,在相近的计算工作量下(顺便提一下,数值求积计算工作量的大小,主要看计算函数值次数的多少),有可能获得较精确的近似值。
的速度就越快,在相近的计算工作量下(顺便提一下,数值求积计算工作量的大小,主要看计算函数值次数的多少),有可能获得较精确的近似值。
例1 利用复合牛顿—柯特斯公式,计算
![]()
的近似值。
解 我们用两种方法进行计算。
先将积分区间![]() 八等分(分点及分点处的函数值见表4-2),用复合梯形公式得
八等分(分点及分点处的函数值见表4-2),用复合梯形公式得
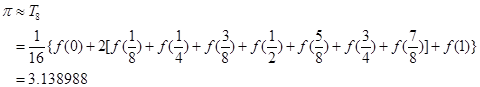
表 4-2
|
|
|
|
0 1/8 1/4 3/8 1/2 |
4.00000000 3.93846154 3.76470588 3.50684932 3.2000000 |
5/8 3/8 7/8 1 |
2.87640449 2.56000000 2.26548673 2.00000000 |
再将积分区间![]() 四等分,用复合辛普生公式得
四等分,用复合辛普生公式得
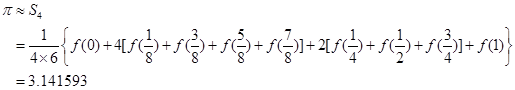
两种方法都用到表4-2中九个点上的函数值,它们的计算工作量基本上相同,但所得结果与积分真值 ![]() 相比较,复合辛普生公式所得近似值S
相比较,复合辛普生公式所得近似值S![]() 远比复合梯形公式所得近似值
远比复合梯形公式所得近似值![]() 要精确。因此,在实际计算时,较多的应用复合辛普生公式。
要精确。因此,在实际计算时,较多的应用复合辛普生公式。
为了便于上机计算,常将复合辛普生公式(4.2.10)改写成
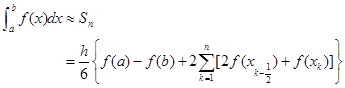
相应的程序框图见图4-3。

图 4-3
4.2.3 误差的事后估计与步长的自动选择
我们虽然可以利用余项公式(4.2.12.)~(4.2.17)来估计近似值的误差,也可根据精度要求用这些公式来确定积分区间的等分数,即确定步长![]() 。但是,由于余项公式中包含有被积函数
。但是,由于余项公式中包含有被积函数![]() 的高阶导数,在具体计算时往往会遇到困难。因此,在实际应用时,常常利用误差的事后估计法来估计近似值的误差,或者确定步长
的高阶导数,在具体计算时往往会遇到困难。因此,在实际应用时,常常利用误差的事后估计法来估计近似值的误差,或者确定步长![]() 。这个方法的大致做法是,将积分区间逐次分半,每分一次就用同一复合求积公式算出相应的积分近似值,并用前后两次计算结果来判断误差的大小。其原理和具体做法如下:
。这个方法的大致做法是,将积分区间逐次分半,每分一次就用同一复合求积公式算出相应的积分近似值,并用前后两次计算结果来判断误差的大小。其原理和具体做法如下:
对于符合梯形公式(4.2.9),由余项公式(4.2.12)或(4.2.15)可以看出,当![]() 在积分区间上变化不大或积分区间
在积分区间上变化不大或积分区间![]() 的等分数
的等分数![]() 较大(即步长
较大(即步长![]() 较小)时,若将
较小)时,若将![]() 的等分数改为
的等分数改为![]() (即将步长缩小到原步长
(即将步长缩小到原步长![]() 的一半),则新近似值
的一半),则新近似值![]() 的余项约为原近似值余项的
的余项约为原近似值余项的![]() ,即
,即
![]()
其中, ![]() 表示积分
表示积分![]() 的真值。对
的真值。对![]() 求解得
求解得
![]() (4.2.20)
(4.2.20)
此式表明,若用![]() 作为积分真值
作为积分真值![]() 的近似值,则其误差约为
的近似值,则其误差约为![]() 。故在将区间逐次分半进行计算的过程中,可以用前后两次计算的结果
。故在将区间逐次分半进行计算的过程中,可以用前后两次计算的结果![]() 和
和![]() 来估计误差与确定步长。具体做法是:先算出
来估计误差与确定步长。具体做法是:先算出![]() 和
和![]() ,若
,若 ![]() (
(![]() 为计算结果的允许误差),则停止计算,并取
为计算结果的允许误差),则停止计算,并取![]() 作为积分的近似值;否则,将区间再次分半后算出新近似值
作为积分的近似值;否则,将区间再次分半后算出新近似值![]() ,并检查不等式
,并检查不等式![]() 是否成立······直到得到满足精度要求的结果为止。
是否成立······直到得到满足精度要求的结果为止。
对于复合辛普生公式(4.2.10)和复合柯特斯公式(4.2.11) ,当所涉及的高阶导数在积分区间上变化不大或积分区间的等分数![]() 较大时,由相应的余项公式可以看出
较大时,由相应的余项公式可以看出
![]() 和
和 ![]()
分别对![]() 求解得
求解得
![]() (4.2.21)
(4.2.21)
![]() (4.2.22)
(4.2.22)
因此,也可以像使用复合梯形法求积分近似值那样,在将积分区间逐次分半进行计算的过程中,估计新近似值![]() 和
和![]() 的误差,并判断计算过程是否需要继续进行下去。
的误差,并判断计算过程是否需要继续进行下去。
上述过程容易在电子计算机上实现。
4.2.4 复合梯形法的递推公式
上面介绍的变步长的计算方案,虽然提供了估计误差与选取步长的简便方法,但是还没有考虑到避免在同一节点上重复计算函数值的问题,故有进一步改进的余地。
先看复合梯形公式。在利用式(4.2.9) 计算![]() 时,需要计算
时,需要计算![]() 个点(它们是积分区间
个点(它们是积分区间![]()
![]() 等分的分点,不妨简称为“
等分的分点,不妨简称为“![]() 分点”)上的函数值。当
分点”)上的函数值。当![]() 不满足精度要求时,根据上面提供的计算方案,就应将各小区间分半,计算出新近似值
不满足精度要求时,根据上面提供的计算方案,就应将各小区间分半,计算出新近似值![]() 。若仍旧利用式(4.2.9) 进行计算
。若仍旧利用式(4.2.9) 进行计算![]() ,就需要求出
,就需要求出![]() 个点(它们是“
个点(它们是“![]() 分点”)上的函数值。而实际上,在这
分点”)上的函数值。而实际上,在这![]() 个
个![]() 分点中,包含有
分点中,包含有![]() 个
个![]() 分点,对应的函数值在计算
分点,对应的函数值在计算![]() 时早已算出,现在重新计算这些点上的函数值,显然是极不合理的。
时早已算出,现在重新计算这些点上的函数值,显然是极不合理的。
为了避免这种重复计算,我们来分析新近似值![]() 与原有近似值
与原有近似值 ![]() 之间的联系。由复合梯形公式(4.2.9)知
之间的联系。由复合梯形公式(4.2.9)知
![]()
若注意到在![]() 分点
分点
![]()
中,当![]() 取偶数时是
取偶数时是![]() 分点,当
分点,当![]() 取奇数时才是新增加的分点,将新增加的分点处的函数值从求和记号中分离出来,就有
取奇数时才是新增加的分点,将新增加的分点处的函数值从求和记号中分离出来,就有
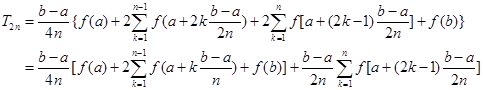
![]()
![]()
由递推公式(4.2.23)可以看出,在已经算出![]() 的基础上在计算
的基础上在计算![]() 时,只要计算
时,只要计算![]() 个新分点上的函数值就行了。与直接利用复合梯形公式(4.2.9)求
个新分点上的函数值就行了。与直接利用复合梯形公式(4.2.9)求![]() 相比较,计算工作量几乎节省了一半。
相比较,计算工作量几乎节省了一半。
例2 利用递推公式(4.2.23)重新计算![]() 的近似值,使误差不超过
的近似值,使误差不超过![]() 。
。
解 我们在积分区间逐次分半的过程中顺次计算积分近似值![]() 并用是否满足不等式
并用是否满足不等式![]() (
(![]() 为计算结果的允许误差,根据题意
为计算结果的允许误差,根据题意![]() )来判断计算过程是否需要继续下去。
)来判断计算过程是否需要继续下去。
先对整个区间![]() 使用梯形公式(4.2.3),得
使用梯形公式(4.2.3),得
![]()
然后将区间二等分,出现的新分点是![]() ,由递推公式(4.2.23)得
,由递推公式(4.2.23)得
![]()
再将各小区间二等分,出现了两个新分点![]() 与
与![]() ,由递推公式(4.2.23)得
,由递推公式(4.2.23)得
![]()
这样,不断将各小区间二分下去,可利用递推公式(4.2.23)依次算出![]() 。计算结果见表4-3。因为
。计算结果见表4-3。因为![]() ,故
,故![]() 为满足精度要求的近似值。
为满足精度要求的近似值。
表 4-3
|
|
|
|
1 2 4 8 16 |
3 3.1 3.13117647 3.13898849 3.14094161 |
32 64 128 256 512 |
3.14142989 3.14155196 3.14158248 3.14159011 3.14159202 |
为了便于上机计算,我们将积分区间![]() 的等分数依次取为
的等分数依次取为![]() (如表4-3),并将递推公式(4.2.23)改写成
(如表4-3),并将递推公式(4.2.23)改写成
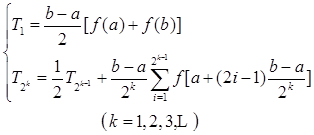 (4.2.24)
(4.2.24)
相应的程序框图见图4-4.其中,![]() 为精度控制量,
为精度控制量,![]() 为最大二分次数(用来控制计算工作量)。
为最大二分次数(用来控制计算工作量)。
对于复合辛普生公式与复合柯特斯公式,我们也可以根据上述原理构造相应的递推公式。但是,下节提供的算法给出了在积分区间逐次分半过程中,近似值![]() 或
或![]() 更为简便的算法,故不再讨论它们。
更为简便的算法,故不再讨论它们。
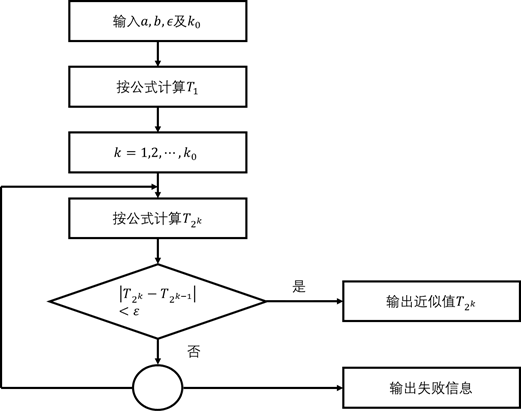
图 4-4
