4.3 龙贝格算法

龙贝格（Romberg）算法是在积分区间逐次分半的过程中，对用复合梯形法产生的近似值进行加权平均，以获得准确程度较高的近似值的一种方法，具有公式简练、使用方便、结果较可靠等优点。本节介绍它的基本原理和应用方法。

4.3.1 龙贝格算法的基本原理

上节中介绍的递推公式（4.2.23）或（4.2.24），虽然具有结构简单，易在电子计算机上实现等优点，但是由它产生的梯形序列，其收敛速度却是非常缓慢的。例如用此法计算的近似值时，要一直算到才获得误差不超过的近似值（见例2）。因此，用这种方法计算更复杂的高精度要求的积分近似值，显然是费时、费力甚至是不可能的。如何提高收敛速度以节约计算工作量，自然是人们极为关心的课题。

我们曾经从近似等式（4.2.20）出发，指出用作为积分真值的近似值，其误差约为。这就启发我们，如果用作为的一种补偿，就可以期望所得到的新近似值

即

                       （4.3.1）

有可能比更好的接近于积分。

如在例2中，

   和  

是两个精度很差的近似值，但如果将它按式（4.3.1）作线性组合，所得到的新近似值

却具有七位有效数字，其准确程度比还要高，而计算只涉及求九个点上的函数值，其计算工作量仅为计算的。

那么，按式（4.3.1）作线性组合得到的新近似值，其实质又是什么呢？通过直接验证，易知亦即

                  （4.3.2）

这表明在收敛速度缓慢的梯形序列的基础上，若将与按式（4.3.2）作线性组合，就可产生收敛速度较快的辛普生序列。

同理，从近似等式（4.2.21）出发，通过类似的分析，可以得到

　　　　            （4.3.3）

故在辛普生序列的基础上，将按式（4.3.3）作线性组合，就可产生收敛速度更快的柯特斯序列。

这种加速过程还可以继续下去。例如，通过与的线性组合

   　　　　　　       （4.3.4）

可以在柯特斯序列的基础上，产生一个称为龙贝格序列的新序列。

经过进一步的分析，可以证明，当满足一定条件时，龙贝格序列比柯特斯序列更快地收敛到积分的真值。

综上可知，我们可以在积分区间逐次分半的过程中利用公式（4.3.2），（4.3.3）和（4.3.4），，将粗糙的近似值逐步地“加工”成越来越精确的近似值。也就是说，将收敛速度缓慢的梯形序列逐步“加工”成收敛速度越来越快的新序列。这种加速的方法就称为龙贝格算法。其加工过程如图4-5，其中圆圈中号码表示计算顺序。

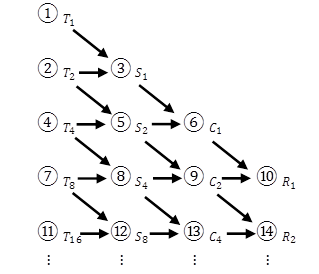
图 4-5

例3 利用公式（4.3.2），（4.3.3）和（4.3.4）“加工”例2中得到的的近似值和，计算结果见表4-4，其中代表二分次数。

由表4-4可以看出，“加工”的效果非常显著，而“加工”的计算量，因只需做少量的四则运算，没有涉及到求函数值，故可以忽略不计。

表4-4

k
0	3
1	3.1	3.133333
2	3.131176	3.141569	3.142118
3	3.138988	3.141593	3.141594	3.141586
4	3.140941	3.141592	3.141592	3.141593

4.3.3龙贝格算法计算公式的简化

为了便于上机计算，我们引用记号来表示各近似值，其中仍代表积分区间的二分次数，而下标则指出了近似值所在序列的性质：当时在梯形序列中，当时在辛普生序列中，当时在柯特斯序列中……例如，表4-4中的各近似值，若用记号表示则如表4-5所示。

表 4-5

引入上面记号后，龙贝格算法所用到的各个计算公式可以统一为

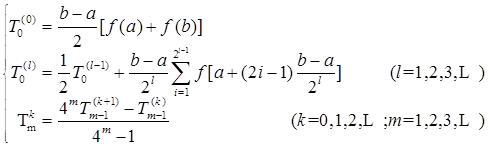
相应的程序框图见图4-6。其中为最大二分次数。

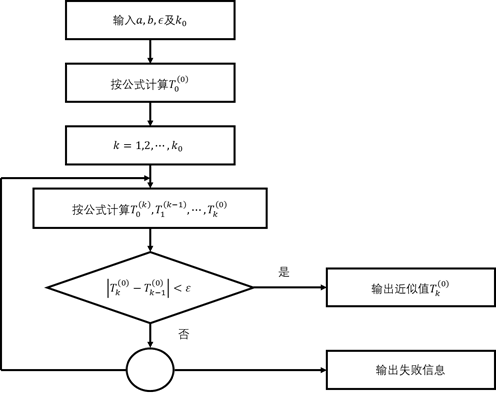
图4-6

最后指出下列几点：

（1）当较大时，由式（4.3.5）的第三式知。因此，在实际计算中，常规定m3，即计算到出现龙贝格序列为止。在这种情况下，程序框图4-6应作相应的修改，需将“按公式（4.3.5）计算”改为“按公式（4.3.5）计算”，并将精度控制法“”改为“”。

（2）为防止假收敛，可设置最小二分次数。当时，跳过精度判别而继续运算。

（3）可以用二维数组来存放与参加运算，也可用一维数组。