内容导入

代数方程求根问题是一个古老的数学问题，早在16世纪就找到了三次、四次方程的求根公式。但直到19世纪才证明n≧5次的一般代数方程式不能用代数公式求解。因此，需要研究用数值方法求得满足一定精度的代数方程式的近似解。

在工程和科学技术中许多问题常常归结为求解非线性方程式问题，例如在控制系统的设计领域、人口增长率的研究等。

例1　关于真实气体的状态方程为

    　　　　           （5.1.1）

其中，是气体压力，是气体体积，是绝对温度，是气体系数。

如果已知某气体的温度及压力，那么求体积的方程为

  　            （5.1.2）

或                       

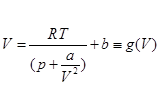
本章将介绍求解这种类型方程的近似解的数值方法。

设有一非线性方程

                           （5.1.3）

其中，为实变量的非线性函数。

内容简介

（1）引入非线性方程数值解的问题；

（2）给出了非线性方程的根的定义和什么是超越方程的定义；

（3）给出了代数基本定理和方程根存在的定理。

（4）给出了求解方程近似根的最简单方法。