内容导入:
解非线性方程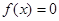 的迭代法是一种将非线性函数数值解的方法。但是其收敛速度比较慢。牛顿方法的最大优点是在方程单根附近具有较高的收敛速度,牛顿方法可用来计算
的迭代法是一种将非线性函数数值解的方法。但是其收敛速度比较慢。牛顿方法的最大优点是在方程单根附近具有较高的收敛速度,牛顿方法可用来计算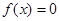 的实根,还可计算代数方程的复根。
的实根,还可计算代数方程的复根。
内容简介
(1)利用导数的近似公式推导出牛顿方法的计算公式;
(2)给出了牛顿计算公式的几何意义;
(3)讨论牛顿法的局部收敛性;
(4)牛顿法的程序实现框图。
(5)牛顿下山法—一种牛顿法的修正方法,即在牛顿法公式中引入了一个因子,使得牛顿法收敛速度加快。
边学边练
习题:用牛顿方法求下述满足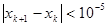 的近似根。
的近似根。
(1)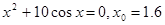 ;(2)
;(2)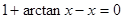 。
。

解:
(1)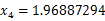
(2)2.13226776