5.1 非线性方程的数值解法引言

代数方程求根问题是一个古老的数学问题，早在16世纪就找到了三次、四次方程的求根公式。但直到19世纪才证明n≧5次的一般代数方程式不能用代数公式求解。因此，需要研究用数值方法求得满足一定精度的代数方程式的近似解。

在工程和科学技术中许多问题常常归结为求解非线性方程式问题，例如在控制系统的设计领域、人口增长率的研究等。

例1　关于真实气体的状态方程为

    　　　　           （5.1.1）

其中，是气体压力，是气体体积，是绝对温度，是气体系数。

如果已知某气体的温度及压力，那么求体积的方程为

     　            （5.1.2）

或                     

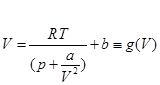
本章将介绍求解这种类型方程的近似解的数值方法。

设有一非线性方程

                          （5.1.3）

其中，为实变量的非线性函数。

定义1 

（1）如果有使得，则称为方程（5.1.3）的根，或称之为函数的零点。

（2）当为多项式时，即方程为

称为n次代数方程。当包含指数函数或三角函数等特殊函数时，称为超越方程。

（3）如果可分为

其中，，为正整数，则称为的重根。当时称为的单根。

本章将介绍计算机上常用的求解非线性方程的近似根的数值方法。

首先叙述两个基本定理。

定理1 （代数基本定理）

设为具有复系数的次代数方程，则于复数域上恰有个根（重根计算个）。如果为实系数代数方程，则复数根成对出现，即当是的复根，则亦是的根。

定理2

（1）设于上连续；

（2）且，则存在有使即于内存在实的零点。

问题：设有非线性实系数方程，需要求出方程的所有实根（或复根）。

求方程的近似根，一般说有这样两个问题：

(1) 根的分离。找出有根的区间（或平面区域），使得在一些较小的区间（平面区域）只有一个根（或一对共轭根），这样可获得方程各根的近似值。

最简单方法是绘出图形，方程的实根就是曲线与轴交点的横坐标，也可采用搜索的方法，来确定根的范围，即从某出发，选取步长，如果有

则在内必有的实根。其中，。

(2) 近似根的精确化。用求方程根的数值方法，使求得的近似根精确化，直到具有足够的精度。

例２　用搜索法确定下述方程在的实根范围。

解   取。

输出：有根区间为（3.3，3.4）且区间（3.6，3.7）内无实根。