5.2 二分法

设有非线性方程

                  （5.2.1）

其中，为上连续函数且设（不妨设方程（5.2.1）于 内仅有一个实根）。

求方程实根的二分法过程，就是将含根区间逐步分半，检查函数值符号的变化，以便确定含根的充分小区间。

二分法叙述如下：记（图5-1）。

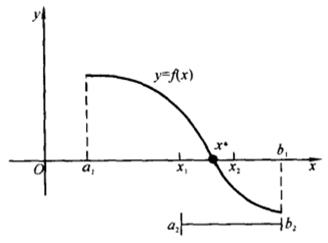
图 5-1

第1步分半计算：将分半，计算中点及，如果

则根一定在区间 内，否则根一定在区间内（若，则）。于是得到长度缩小一半的含根区间，即

，且

第步分半计算：重复上述过程，设已完成第1步，…，第步分半计算得到含根区间

且满足：

（1），即；

（2）；

现进行第步分半计算：

（3）计算，且有

      　　 　　　　　　　　  （5.2.2）

（4）确定新的含根区间，即如果，则根一定在内，否则根一定在区间，且有

总之，由上述二分法得到一序列，由式（5.2.2），则有

可用二分法求方程实根的近似值到任意指定的精度。事实上，设为给定精度要求，是确定分半次数使

由，两边取对数，即得

      　     　　　　　　(5.2.3)

定理3 （二分法）

给定方程，设于上连续，且，则由二分法产生序列收敛于方程的根，且具有性质　　

例3 用二分法求于 内的一个实根，且要求精确到小数后第3位（即要求）。显然，。

解   由，由公式（5.2.3）可确定所需分半次数。计算结果如表5-1。

表 5-1

二分法的优点是方法简单，且对只要求连续即可。可用二分法求出于内的全部实根。但二分法不能求复根即偶数重根。

二分法框图如图5-2所示

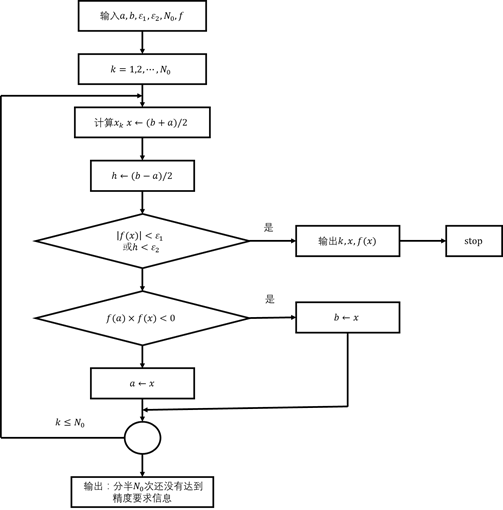
图5-2

二分法：设方程，其中于 上连续，且满足条件（且设于内只有一个实根）。

(1)计算；

(2)如果或，则输出；

(3)如果则，否则

其中，表示给定的最大分半次数，当或时分半终止。